
【題目】對于定義域為![]() 上的函數
上的函數![]() ,如果同時滿足下列三條:
,如果同時滿足下列三條:
(1)對任意的![]() ,總有
,總有![]() ;(2)若
;(2)若![]() ,
, ![]() ,都有
,都有![]()
![]() 成立;
成立;
(3)若![]() ,則
,則![]() .則稱函數
.則稱函數![]() 為超級囧函數.
為超級囧函數.
則下列是超級囧函數的為_____________________.
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .
.
【答案】(3)
【解析】對于(1)不滿足①對任意的x∈[0,+∞),總有f(x)≥0,故(1)不是超級囧函數;
對于(2),g(x)=![]() (x∈[0,1]),則g(x1+x2),g(x+1)可能沒意義,故故(2)不是超級囧函數;
(x∈[0,1]),則g(x1+x2),g(x+1)可能沒意義,故故(2)不是超級囧函數;
對于(3),函數h(x)=2x﹣1(x∈[0,+∞)上滿足h(x)≥0,
若x1≥0,x2≥0,x1+x2≤1,則h(x1+x2)﹣[h(x1)+h(x2)]=2x1+x2﹣1﹣[(2x1﹣1)+(2x2﹣1)
=2x1+x2﹣2x1﹣2x2+1)=(2x1﹣1)(2x2﹣1)≥0,
即h(x1+x2)≥h(x1)+h(x2),
要滿足0≤x1<x2<1,則![]() >1,只需f(x1+1)﹣f(x2﹣1)<(x1+1)﹣(x2+1),即函數G(t)=f(t)﹣t在[1,2)上遞增即可.函數h(x)=2x﹣1顯然滿足,故(3)是超級囧函數;
>1,只需f(x1+1)﹣f(x2﹣1)<(x1+1)﹣(x2+1),即函數G(t)=f(t)﹣t在[1,2)上遞增即可.函數h(x)=2x﹣1顯然滿足,故(3)是超級囧函數;
對于(4),x1≥0,x2≥0時,p(x1+x2)﹣[p(x1)+p(x2)]=ln![]() =ln
=ln![]() ≤0,故不滿足②若x1≥0,x2≥0,都有f(x1+x2)≥f(x1)+f(x2)成立,故(4)不是超級囧函數;
≤0,故不滿足②若x1≥0,x2≥0,都有f(x1+x2)≥f(x1)+f(x2)成立,故(4)不是超級囧函數;
故答案為:(3)


科目:高中數學 來源: 題型:
【題目】設曲線y=xn+1(n∈N*)在點(1,1)處的切線與x軸的交點的橫坐標為xn , 則log2017x1+log2017x2+…+log2017x2016的值為( )
A.﹣log20172016
B.﹣1
C.log20172016﹣1
D.1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業人力資源部為了研究企業員工工作積極性和對待企業改革態度的關系,隨機抽取了72名員工進行調查,所得的數據如表所示:
積極支持改革 | 不太支持改革 | 合 計 | |
工作積極 | 28 | 8 | 36 |
工作一般 | 16 | 20 | 36 |
合 計 | 44 | 28 | 72 |
對于人力資源部的研究項目,根據上述數據能得出的結論是
(參考公式與數據: ![]() .當Χ2>3.841時,有95%的把握說事件A與B有關;當Χ2>6.635時,有99%的把握說事件A與B有關; 當Χ2<3.841時認為事件A與B無關.)( )
.當Χ2>3.841時,有95%的把握說事件A與B有關;當Χ2>6.635時,有99%的把握說事件A與B有關; 當Χ2<3.841時認為事件A與B無關.)( )
A.有99%的把握說事件A與B有關
B.有95%的把握說事件A與B有關
C.有90%的把握說事件A與B有關
D.事件A與B無關
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x+lg ![]() +x)的定義域是R.
+x)的定義域是R.
(1)判斷f(x)在R上的單調性,并證明;
(2)若不等式f(m3x)+f(3x﹣9x﹣4)<0對任意x∈R恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A={x|x2﹣3x﹣4≤0},B={x|x2﹣2mx+m2﹣9≤0},C={y|y=ax+b,a>0,且a≠1,x∈R}.
(1)若A∩B=[0,4],求m的值;
(2)若A∩C只有一個子集,求b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】要在墻上開一個上部為半圓,下部為矩形的窗戶(如圖所示),在窗框總長度為l的條件下, 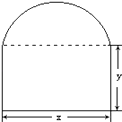
(1)請寫出窗戶的面積S與圓的直徑x的函數關系;
(2)要使窗戶透光面積最大,窗戶應具有怎樣的尺寸?并寫出最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2+bx+c(a,b,c∈R且a≠0),若對任意實數x,不等式2x≤f(x) ![]() (x+1)2恒成立.
(x+1)2恒成立.
(1)求f(1)的值;
(2)求a的取值范圍;
(3)若函數g(x)=f(x)+2a|x﹣1|,x∈[﹣2,2]的最小值為﹣1,求a的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com