
【題目】某工廠為生產一種精密管件研發了一臺生產該精密管件的車床,該精密管件有內外兩個口徑,監管部門規定“口徑誤差”的計算方式為:管件內外兩個口徑實際長分別為![]() ,標準長分別為
,標準長分別為![]() 則“口徑誤差”為
則“口徑誤差”為![]() 只要“口徑誤差”不超過
只要“口徑誤差”不超過![]() 就認為合格,已知這臺車床分晝夜兩個獨立批次生產.工廠質檢部在兩個批次生產的產品中分別隨機抽取40件作為樣本,經檢測其中晝批次的40個樣本中有4個不合格品,夜批次的40個樣本中有10個不合格品.
就認為合格,已知這臺車床分晝夜兩個獨立批次生產.工廠質檢部在兩個批次生產的產品中分別隨機抽取40件作為樣本,經檢測其中晝批次的40個樣本中有4個不合格品,夜批次的40個樣本中有10個不合格品.
(Ⅰ)以上述樣本的頻率作為概率,在晝夜兩個批次中分別抽取2件產品,求其中恰有1件不合格產品的概率;
(Ⅱ)若每批次各生產1000件,已知每件產品的成本為5元,每件合格品的利潤為10元;若對產品檢驗,則每件產品的檢驗費用為2.5元;若有不合格品進入用戶手中,則工廠要對用戶賠償,這時生產的每件不合格品工廠要損失25元.以上述樣本的頻率作為概率,以總利潤的期望值為決策依據,分析是否要對每個批次的所有產品作檢測?
【答案】(Ⅰ)![]() ;(Ⅱ)晝批次不做檢測為好;夜批次做檢測為優.
;(Ⅱ)晝批次不做檢測為好;夜批次做檢測為優.
【解析】
(Ⅰ)先分別求出晝批次和夜批次合格品的概率,再由獨立事件同時發生的概率公式,即可求解;
(Ⅱ)分別求出晝批次和夜批次不做檢測的利潤期望值和都做檢測的利潤期望值,加以對比,即可得出結論.
(Ⅰ)以樣本的頻率作為概率,在晝批次中隨機抽取1件為合格品的概率是![]() ,
,
在夜批次中隨機抽取1件為合格品的概率是![]() ,
,
故兩個批次中分別抽取2件產品,其中恰有1件不合格產品的概率為![]() .
.
(Ⅱ)①若對所有產品不做檢測,
設![]() 為晝批次中隨機抽取1件的利潤,
為晝批次中隨機抽取1件的利潤,![]() 的可能取值為10,
的可能取值為10,![]() ,
,
所以![]() 的分布列為
的分布列為
| 10 |
|
| 0.9 | 0.1 |
所以![]() ,
,
故在不對所有產品做檢測的情況下,
1000件產品的利潤的期望值為![]() ,
,
設![]() 為夜批次中隨機抽取1件的利潤,
為夜批次中隨機抽取1件的利潤,![]() 的可能取值為10,
的可能取值為10,![]() ,
,
所以![]() 的分布列為
的分布列為
| 10 |
|
| 0.75 | 0.25 |
所以![]() ,
,
故在不對所有產品做檢測的情況下,
1000件產品的利潤的期望值為![]() ,
,
②若對所有產品做檢測,
晝批次1000件產品的合格品的期望為900件,不合格品的期望為100件,
所以利潤為![]() ,
,
夜批次1000件產品的合格品的期望為750件,不合格品的期望為250件,
所以利潤為![]() ,
,
綜上,晝批次不做檢測的利潤期望6500大于做檢測的利潤期望6000,
故晝批次不做檢測為好;
夜批次不做檢測的利潤期望1250小于做檢測的利潤期望3750,
故夜批次做檢測為優.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】學校水果店有蘋果、梨、香蕉、石榴、橘子、葡萄、西柚等![]() 種水果,西柚數量不多,只夠一個人購買,甲乙丙丁戊
種水果,西柚數量不多,只夠一個人購買,甲乙丙丁戊![]() 位同學去購買,每人只能選擇其中一種,這
位同學去購買,每人只能選擇其中一種,這![]() 位同學購買后,恰好買了其中三種水果,則他們購買水果的可能情況有___________種.
位同學購買后,恰好買了其中三種水果,則他們購買水果的可能情況有___________種.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,動圓
,動圓![]() 與圓
與圓![]() 外切,且與直線
外切,且與直線![]() 相切,該動圓圓心
相切,該動圓圓心![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程
的方程
(2)過點![]() 的直線與拋物線相交于
的直線與拋物線相交于![]() 兩點,拋物線在點A的切線與
兩點,拋物線在點A的切線與![]() 交于點N,求
交于點N,求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() ,
,![]() 分別是
分別是![]() ,
,![]() 上的動點,將矩形
上的動點,將矩形![]() 沿
沿![]() 所在的直線進行隨意翻折,在翻折過程中直線
所在的直線進行隨意翻折,在翻折過程中直線![]() 與直線
與直線![]() 所成角的范圍(包含初始狀態)為( )
所成角的范圍(包含初始狀態)為( )
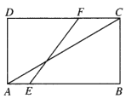
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,橢圓![]() 的左、右頂點分別為A、B,右焦點為F,且點F滿足
的左、右頂點分別為A、B,右焦點為F,且點F滿足![]() ,由橢圓C的四個頂點圍成的四邊形面積為
,由橢圓C的四個頂點圍成的四邊形面積為![]() .過點
.過點![]() 的直線TA,TB與此橢圓分別交于點
的直線TA,TB與此橢圓分別交于點![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() .
.
(1)求橢圓C的標準方程;
(2)當T在直線![]() 時,直線MN是否過x軸上的一定點?若是,求出該定點的坐標;若不是,請說明理由.
時,直線MN是否過x軸上的一定點?若是,求出該定點的坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為評估![]() 設備生產某種零件的性能,從該設備生產零件的流水線上隨機抽取100件零件作為樣本,測量其直徑后,整理得到下表:
設備生產某種零件的性能,從該設備生產零件的流水線上隨機抽取100件零件作為樣本,測量其直徑后,整理得到下表:
直徑/ | 78 | 79 | 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 | 91 | 93 | 合計 |
件數 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
經計算,樣本的平均值![]() ,標準差
,標準差![]() ,以頻率值作為概率的估計值.
,以頻率值作為概率的估計值.
(1)為評判一臺設備的性能,從該設備加工的零件中任意抽取一件,記其直徑為![]() ,并根據以下不等式進行評判(
,并根據以下不等式進行評判(![]() 表示相應事件的頻率):
表示相應事件的頻率):
①![]() ;②
;②![]() ;③
;③![]() ,評判規則為:若同時滿足上述三個不等式,則設備等級為甲;僅滿足其中兩個,則等級為乙;若僅滿足其中一個,則等級為丙;若全部不滿足,則等級為丁.試判斷
,評判規則為:若同時滿足上述三個不等式,則設備等級為甲;僅滿足其中兩個,則等級為乙;若僅滿足其中一個,則等級為丙;若全部不滿足,則等級為丁.試判斷![]() 設備的性能等級.
設備的性能等級.
(2)將直徑小于等于![]() 的零件或直徑大于等于
的零件或直徑大于等于![]() 的零件認定為是“次品”,將直徑小于等于
的零件認定為是“次品”,將直徑小于等于![]() 的零件或直徑大于等于
的零件或直徑大于等于![]() 的零件認定為是“突變品”,從樣本的“次品”中隨意抽取2件零件,求“突變品”個數
的零件認定為是“突變品”,從樣本的“次品”中隨意抽取2件零件,求“突變品”個數![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在等比數列![]() 中,已知
中,已知![]() 設數列
設數列![]() 的前n項和為
的前n項和為![]() ,且
,且![]()
(1)求數列![]() 通項公式;
通項公式;
(2)證明:數列![]() 是等差數列;
是等差數列;
(3)是否存在等差數列![]() ,使得對任意
,使得對任意![]() ,都有
,都有![]() ?若存在,求出所有符合題意的等差數列
?若存在,求出所有符合題意的等差數列![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2|x+1|+|x-2|.
(1)求f(x)的最小值m;
(2)若a,b,c均為正實數,且滿足a+b+c=m,求證:![]() +
+![]() +
+![]() ≥3.
≥3.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小區內有一塊以![]() 為圓心半徑為20米的圓形區域.廣場,為豐富市民的業余文化生活,現提出如下設計方案:如圖,在圓形區域內搭建露天舞臺,舞臺為扇形
為圓心半徑為20米的圓形區域.廣場,為豐富市民的業余文化生活,現提出如下設計方案:如圖,在圓形區域內搭建露天舞臺,舞臺為扇形![]() 區域,其中兩個端點
區域,其中兩個端點![]() ,
,![]() 分別在圓周上;觀眾席為梯形
分別在圓周上;觀眾席為梯形![]() 內且在圓
內且在圓![]() 外的區域,其中
外的區域,其中![]() ,
,![]() ,且
,且![]() ,
,![]() 在點
在點![]() 的同側.為保證視聽效果,要求觀眾席內每一個觀眾到舞臺
的同側.為保證視聽效果,要求觀眾席內每一個觀眾到舞臺![]() 處的距離都不超過60米.設
處的距離都不超過60米.設![]() .
.

(1)求![]() 的長(用
的長(用![]() 表示);
表示);
(2)對于任意![]() ,上述設計方案是否均能符合要求?
,上述設計方案是否均能符合要求?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com