
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的單調性;
的單調性;
(2)當![]() 時,若函數
時,若函數![]() 的極值為e,求
的極值為e,求![]() 的值;
的值;
(3)當![]() 時,若
時,若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;(2)
上單調遞增;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先求導,根據導數和函數單調性的關系即可求出,
(2)根據導數和函數的極值的關系即可求出,
(3)根據函數的單調性和端點值以及最值,分類討論即可求出.
(1)當![]() ,
,![]() ,
,
![]() ,
,
由![]() 得
得![]() ,解得
,解得![]() ,
,
由![]() 得
得![]() ,解得
,解得![]() ,
,
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
(2)![]() ,
,
因![]() ,所以由
,所以由![]() 得
得![]() ,解得
,解得![]() ,
,
所以![]() 在
在![]() 上單調遞增,可知
上單調遞增,可知![]() 在
在![]() 上單調遞減;
上單調遞減;
所以函數![]() 有極大值,無極小值,得極人值
有極大值,無極小值,得極人值![]() ,
,
即![]() ,而
,而![]() 顯然為增函數.
顯然為增函數.
又![]() ,所以
,所以![]() ,得
,得![]() .
.
(3)法一:![]() (*),
(*),
①當![]() 時,
時,
過程一:由(*)式得![]() ,得
,得![]() .
.
而![]() 在
在![]() 上單調遞減,
上單調遞減,![]() ,上式不可能恒成立;
,上式不可能恒成立;
過程二:![]() ,
,![]() ,
,
可知(*)式不成立;
②當![]() 時,由(*)式得
時,由(*)式得![]() ,得
,得![]() .
.
而![]() ,由上式恒成立得
,由上式恒成立得![]() ;
;
綜上知![]() .
.


科目:高中數學 來源: 題型:
【題目】美國一貫推行強權政治,2018年3月22日,美國總統特朗普在白宮簽署了對中國輸美產品征收關稅的總統備忘錄,限制中國商品進入美國市場。中國某企業計劃打入美國市場,決定從A、B兩種產品中只選一種進行投資生產,已知投入生產這兩種產品的有關數據如下表:(單位:萬元)
年固定成本 | 每件產品成本 | 每件產品銷售價 | 每年最多可生產件數 | |
A產品 | 40 | m | 15 | 200 |
B產品 | 60 | 10 | 22 | 150 |
其中固定成本與年生產的件數無關,m是待定的常數,其值由生產A產品的原材料決定,預計![]() ,另外,年銷售
,另外,年銷售![]() 件B產品時需交0.05
件B產品時需交0.05![]() 萬元的附件關稅,假設生產出來的產品都能在當年銷售出去.
萬元的附件關稅,假設生產出來的產品都能在當年銷售出去.
(1)求該廠分別投資生產A、B兩種產品的年利潤![]() 與生產相應產品的件數
與生產相應產品的件數![]() 之間的函數關系,并求出其定義域;
之間的函數關系,并求出其定義域;
(2)如何投資才可獲得最大年利潤?請設計出投資方案.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商店為了更好地規劃某種商品進貨的量,該商店從某一年的銷售數據中,隨機抽取了![]() 組數據作為研究對象,如下圖所示(
組數據作為研究對象,如下圖所示(![]() (噸)為該商品進貨量,
(噸)為該商品進貨量, ![]() (天)為銷售天數):
(天)為銷售天數):
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅰ)根據上表數據在下列網格中繪制散點圖;
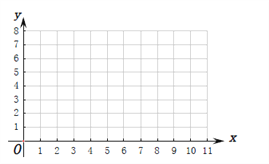
(Ⅱ)根據上表提供的數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(Ⅲ)在該商品進貨量![]() (噸)不超過6(噸)的前提下任取兩個值,求該商品進貨量
(噸)不超過6(噸)的前提下任取兩個值,求該商品進貨量![]() (噸)恰有一個值不超過3(噸)的概率.
(噸)恰有一個值不超過3(噸)的概率.
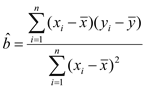 ,
,查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一袋中有大小相同的4個紅球和2個白球,給出下列結論:
①從中任取3球,恰有一個白球的概率是![]() ;
;
②從中有放回的取球6次,每次任取一球,則取到紅球次數的方差為![]() ;
;
③現從中不放回的取球2次,每次任取1球,則在第一次取到紅球的條件下,第二次再次取到紅球的概率為![]() ;
;
④從中有放回的取球3次,每次任取一球,則至少有一次取到紅球的概率為![]() .
.
其中所有正確結論的序號是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將4名志愿者分別安排到火車站、輪渡碼頭、機場工作,要求每一個地方至少安排一名志愿者,其中甲、乙兩名志愿者不安排在同一個地方工作,則不同的安排方法共有
A. 24種B. 30種C. 32種D. 36種
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com