
【題目】算籌是在珠算發明以前我國獨創并且有效的計算工具,為我國古代數學的發展做出了很大貢獻.在算籌記數法中,以“縱式”和“橫式”兩種方式來表示數字,如下表:
數字形式 |
|
|
|
|
|
|
|
|
|
縱式 |
|
|
|
|
|
|
|
|
|
橫式 |
|
|
|
|
|
|
|
|
|
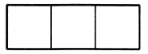
表示多位數時,個位用縱式,十位用橫式,百位用縱式,千位用橫式,以此類推,遇零則置空,如圖所示.如果把![]() 根算籌以適當的方式全部放入下面的表格中,那么可以表示的三位數的個數為______.
根算籌以適當的方式全部放入下面的表格中,那么可以表示的三位數的個數為______.
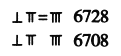
 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:高中數學 來源: 題型:
【題目】已知![]() ,將
,將![]() 的圖像向右平移
的圖像向右平移![]() 個單位后,再保持縱坐標不變,橫坐標變為原來的2倍,得到函數
個單位后,再保持縱坐標不變,橫坐標變為原來的2倍,得到函數![]() 的圖象.
的圖象.
(1)求函數![]() 在
在![]() 上的值域及單調遞增區間;
上的值域及單調遞增區間;
(2)若![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將直角三角形![]() 沿斜邊上的高
沿斜邊上的高![]() 折成
折成![]() 的二面角,已知直角邊
的二面角,已知直角邊![]() ,那么下面說法正確的是_________.
,那么下面說法正確的是_________.
(1) 平面![]() 平面
平面![]() (2)四面體
(2)四面體![]() 的體積是
的體積是![]()
(3)二面角![]() 的正切值是
的正切值是![]() (4)
(4)![]() 與平面
與平面![]() 所成角的正弦值是
所成角的正弦值是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為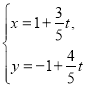 (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,點
兩點,點![]() 的極坐標為
的極坐標為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代著名數學經典,其中對勾股定理的論述,比西方早一千多年,其中有這樣一個問題:“今有圓材埋在壁中,不知大小;以鋸鋸之,深一寸,鋸道長一尺,問徑幾何?”其意為:今有一圓柱形木材,埋在墻壁中,不知其大小,用鋸去鋸該材料,鋸口深1寸,鋸道長1尺,問這塊圓柱形木料的直徑是多少?長為0.5丈的圓柱形木材部分鑲嵌在墻體中,截面圖如圖所示(陰影部分為鑲嵌在墻體內的部分).己知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算該木材鑲嵌墻內部分的體積約為( )(注:一丈=10尺=100寸,
寸,估算該木材鑲嵌墻內部分的體積約為( )(注:一丈=10尺=100寸,![]() )
)
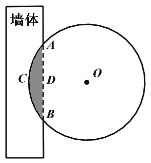
A.300立方寸B.305.6立方寸C.310立方寸D.316.6立方寸
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com