
【題目】已知函數![]() .
.
(1)若![]() 在
在![]() 上為增函數,求實數
上為增函數,求實數![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,函數
時,函數![]() 有零點,求實數
有零點,求實數![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)0.
;(2)0.
【解析】試題分析:(1)![]() 在
在![]() 上為增函數,等價于
上為增函數,等價于![]() 在
在![]() 上恒成立,分類討論,當
上恒成立,分類討論,當![]() 時,由函數
時,由函數![]() 的定義域可知,必須有
的定義域可知,必須有![]() 對
對![]() 恒成立,故只能
恒成立,故只能![]() ,所以
,所以![]() 在
在![]() 上恒成立,構造函數
上恒成立,構造函數![]() ,要使
,要使![]() 在
在![]() 上恒成立,只要
上恒成立,只要![]() 即可,從而可求實數
即可,從而可求實數![]() 的取值范圍;(2)當
的取值范圍;(2)當![]() 時,方程
時,方程![]() 有實根,等價于
有實根,等價于![]() 在
在![]() 上有解,即求
上有解,即求![]() 的值域.構造
的值域.構造![]() (
(![]() ),證明
),證明![]() 在
在![]() 上為增函數,在
上為增函數,在![]() 上為減函數,即可得出結論.
上為減函數,即可得出結論.
試題解析:(1)∵函數![]() 在區間
在區間![]() 上為增函數,
上為增函數,
∴![]() 在區間
在區間![]() 上恒成立,
上恒成立,
①當![]() 時,
時,![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() 在
在![]() 上為增函數,故
上為增函數,故![]() 符合題意.
符合題意.
②當![]() 時,由函數
時,由函數![]() 的定義域可知
的定義域可知![]() 對
對![]() 恒成立,
恒成立,
故只能![]() ,∴
,∴![]() 在
在![]() 上恒成立,
上恒成立,
令函數![]() ,其對稱軸為
,其對稱軸為![]() ,
,
∵![]() ,∴
,∴![]() ,要使
,要使![]() 在
在![]() 上恒成立,只要
上恒成立,只要![]() 即可,
即可,
即![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,綜上所述,
,綜上所述,![]() 的取值范圍為
的取值范圍為![]() .
.
(2)當![]() 時,函數
時,函數![]() 有零點等價于方程:
有零點等價于方程:
![]() 有實根,
有實根,![]() 可化為:
可化為:
![]() .
.
等價于![]() 在
在![]() 上有解,
上有解,
即求函數![]() 的值域,
的值域,
∵函數![]() ,
,
令函數![]() ,則
,則![]() ,
,
∴當![]() 時,
時,![]() ,從而函數
,從而函數![]() 在
在![]() 上為增函數,
上為增函數,
當![]() 時,
時,![]() ,從而函數
,從而函數![]() 在
在![]() 上為減函數,
上為減函數,
因此![]() ,而
,而![]() ,∴
,∴![]() ,
,
故當![]() 時,
時,![]() 取得最大值0.
取得最大值0.


 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:高中數學 來源: 題型:
【題目】線段AB的兩端在直二面角α-l-β的兩個面內,并與這兩個面都成30°角,則異面直線AB與l所成的角是( )
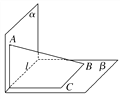
A. 30° B. 45°
C. 60° D. 75°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場經營一批進價為![]() 元/臺的小商品,經調查得知如下數據.若銷售價上下調整,銷售量和利潤大體如下:
元/臺的小商品,經調查得知如下數據.若銷售價上下調整,銷售量和利潤大體如下:
銷售價( |
|
|
|
|
日銷售量( |
|
|
|
|
日銷售額( |
| |||
日銷售利潤( |
|
(1)在下面給出的直角坐標系中,根據表中的數據描出實數對![]() 的對應點,并寫出
的對應點,并寫出![]() 與
與![]() 的一個函數關系式;
的一個函數關系式;
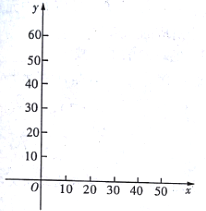
(2)請把表中的空格里的數據填上;
(3)根據表中的數據求![]() 與
與![]() 的函數關系式,并指出當銷售單價為多少元時,才能獲得最大日銷售利潤?
的函數關系式,并指出當銷售單價為多少元時,才能獲得最大日銷售利潤?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數![]() ,若在定義域內存在實數
,若在定義域內存在實數![]() ,滿足
,滿足![]() ,則稱為“局部奇函數”
,則稱為“局部奇函數”
(1)已知二次函數![]() (
(![]() 且
且![]() ),試判斷
),試判斷![]() 是否為“局部奇函數”,并說明理由;
是否為“局部奇函數”,并說明理由;
(2)若![]() 是定義在區間
是定義在區間![]() 上的“局部奇函數”,求實數
上的“局部奇函數”,求實數![]() 的取值范圍;
的取值范圍;
(3)若![]() 為定義域為
為定義域為![]() 上的“局部奇函數”,求實數
上的“局部奇函數”,求實數![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設A是實數集,滿足若a∈A,則![]() ∈A,a≠1,且1A.
∈A,a≠1,且1A.
(1)若2∈A,則集合A中至少還有幾個元素?求出這幾個元素.
(2)集合A中能否只含有一個元素?請說明理由.
(3)若a∈A,證明:1-![]() ∈A.
∈A.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義滿足“如果a∈A,b∈A,那么a±b∈A,且ab∈A,且![]() ∈A(b≠0)”的集合A為“閉集”.試問數集N,Z,Q,R是否分別為“閉集”?若是,請說明理由;若不是,請舉反例說明.
∈A(b≠0)”的集合A為“閉集”.試問數集N,Z,Q,R是否分別為“閉集”?若是,請說明理由;若不是,請舉反例說明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是長方形,側棱
是長方形,側棱![]() 底面
底面![]() ,且
,且![]() ,過D作
,過D作![]() 于F,過F作
于F,過F作![]() 交 PC于E.
交 PC于E.
(Ⅰ)證明:![]() 平面PBC;
平面PBC;
(Ⅱ)求平面![]() 與平面
與平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
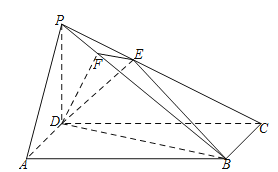
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com