
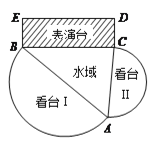
【題目】在一水域上建一個演藝廣場.演藝廣場由看臺Ⅰ,看臺Ⅱ,三角形水域![]() ,及矩形表演臺
,及矩形表演臺![]() 四個部分構(gòu)成(如圖).看臺Ⅰ,看臺Ⅱ是分別以
四個部分構(gòu)成(如圖).看臺Ⅰ,看臺Ⅱ是分別以![]() ,
, ![]() 為直徑的兩個半圓形區(qū)域,且看臺Ⅰ的面積是看臺Ⅱ的面積的3倍;矩形表演臺
為直徑的兩個半圓形區(qū)域,且看臺Ⅰ的面積是看臺Ⅱ的面積的3倍;矩形表演臺![]() 中,
中, ![]() 米;三角形水域
米;三角形水域![]() 的面積為
的面積為![]() 平方米.設(shè)
平方米.設(shè)![]() .
.
(Ⅰ)當(dāng)![]() 時,求
時,求![]() 的長;
的長;
(Ⅱ)若表演臺每平方米的造價為![]() 萬元,求表演臺的最低造價.
萬元,求表演臺的最低造價.
【答案】(Ⅰ)40;(Ⅱ)120萬元.
【解析】試題分析:(1)根據(jù)看臺的面積比得出AB,AC的關(guān)系,代入三角形的面積公式求出AB,AC,再利用余弦定理計算BC;(2)根據(jù)(1)得出造價關(guān)于θ的函數(shù),利用導(dǎo)數(shù)判斷函數(shù)的單調(diào)性求出最小造價
解析:
(Ⅰ)因為看臺Ⅰ的面積是看臺Ⅱ的面積的3倍,所以![]() .
.
在△![]() 中,
中, ![]() ,所以
,所以![]() .
.
由余弦定理可得![]()
![]() ,即
,即![]()
所以 ![]() ,
, ![]() . 當(dāng)
. 當(dāng)![]() 時,
時, ![]()
(Ⅱ)設(shè)表演臺的總造價為![]() 萬元.因為
萬元.因為![]() m,表演臺每平方米的造價為0.3萬元,所以
m,表演臺每平方米的造價為0.3萬元,所以![]() ,
, ![]() .
.
記![]() ,
, ![]() .則
.則![]() .
.
由![]() ,解得
,解得![]() .
.
當(dāng)![]() 時,
時, ![]() ;當(dāng)
;當(dāng)![]() 時,
時, ![]() .
.
故![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,
上單調(diào)遞增,
從而當(dāng)![]() 時,
時, ![]() 取得最小值,最小值為
取得最小值,最小值為![]() . 所以
. 所以![]() (萬元).
(萬元).


科目:高中數(shù)學(xué) 來源: 題型:
【題目】某中學(xué)高三文科班學(xué)生參加了數(shù)學(xué)與地理水平測試,學(xué)校從測試合格的學(xué)生中隨機抽取100人的成績進(jìn)行統(tǒng)計分析.抽取的100人的數(shù)學(xué)與地理的水平測試成績?nèi)缦卤恚?/span>

成績分為優(yōu)秀、良好、及格三個等級,橫向、縱向分別表示地理成績與數(shù)學(xué)成績,例如:表中數(shù)學(xué)成績?yōu)榱己玫墓灿?0+18+4=42人.
(1)若在該樣本中,數(shù)學(xué)成績優(yōu)秀率為30%,求a,b的值;
(2)若樣本中![]() ,求在地理成績及格的學(xué)生中,數(shù)學(xué)成績優(yōu)秀的人數(shù)比及格的人數(shù)少的概率.
,求在地理成績及格的學(xué)生中,數(shù)學(xué)成績優(yōu)秀的人數(shù)比及格的人數(shù)少的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (a為常數(shù))有兩個極值點.
(a為常數(shù))有兩個極值點.
(1)求實數(shù)a的取值范圍;
(2)設(shè)f(x)的兩個極值點分別為x1,x2,若不等式f(x1)+f(x2)<λ(x1+x2)恒成立,求λ的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
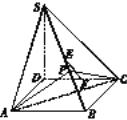
【題目】四棱錐S-ABCD中的底面是菱形,∠BAD=60°,SD⊥底面ABCD,SD=AB=2,E、F分別為SB、CD的中點.
(Ⅰ)求證:EF∥平面SAD;
(Ⅱ)點P是SB上一點,若SB⊥平面APC,試確定點P的位置.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(1)選修4-2:矩陣與變換
求矩陣![]() 的特征值和特征向量.
的特征值和特征向量.
(2)選修4-4:坐標(biāo)系與參數(shù)方程
在極坐標(biāo)系中,圓![]() 的方程為
的方程為![]() ,以極點為坐標(biāo)原點,極軸為
,以極點為坐標(biāo)原點,極軸為![]() 軸的正半軸建立平面直角坐標(biāo)系,圓
軸的正半軸建立平面直角坐標(biāo)系,圓![]() 的參數(shù)方程
的參數(shù)方程![]() (
(![]() 是參數(shù)),若圓
是參數(shù)),若圓![]() 與圓
與圓![]() 相切,求實數(shù)
相切,求實數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(導(dǎo)學(xué)號:05856306)
在△ABC中,內(nèi)角A,B,C的對邊分別為a,b,c,已知![]() ,且b=5,acos C=-1.
,且b=5,acos C=-1.
(Ⅰ)求角A;
(Ⅱ)求△ABC的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某高科技企業(yè)生產(chǎn)產(chǎn)品A和產(chǎn)品B需要甲、乙兩種新型材料.生產(chǎn)一件產(chǎn)品A需要甲材料1.5 kg,乙材料1 kg,用5個工時;生產(chǎn)一件產(chǎn)品B需要甲材料0.5 kg,乙材料0.3 kg,用3個工時,生產(chǎn)一件產(chǎn)品A的利潤為2100元,生產(chǎn)一件產(chǎn)品B的利潤為900元.該企業(yè)現(xiàn)有甲材料150 kg,乙材料90 kg,則在不超過600個工時的條件下,生產(chǎn)產(chǎn)品A、產(chǎn)品B的利潤之和的最大值為______元.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
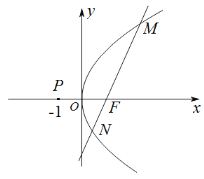
【題目】已知點![]() 為拋物線C:
為拋物線C:![]() 的焦點,過點
的焦點,過點![]() 的動直線
的動直線![]() 與拋物線C交于
與拋物線C交于![]() ,
,![]() 兩點,如圖.當(dāng)直線
兩點,如圖.當(dāng)直線![]() 與
與![]() 軸垂直時,
軸垂直時,![]() .
.
(1)求拋物線C的方程;
(2)已知點![]() ,設(shè)直線PM的斜率為
,設(shè)直線PM的斜率為![]() ,直線PN的斜率為
,直線PN的斜率為![]() .請判斷
.請判斷![]() 是否為定值,若是,寫出這個定值,并證明你的結(jié)論;若不是,說明理由.
是否為定值,若是,寫出這個定值,并證明你的結(jié)論;若不是,說明理由.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com