
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為平行四邊形,
為平行四邊形, ![]() ,
, ![]() ,
, ![]() 底面
底面![]() .
.
(1)證明: ![]() ;
;
(2)設(shè)![]() ,求點(diǎn)
,求點(diǎn)![]() 到面
到面![]() 的距離.
的距離.

【答案】(1)見解析(2)![]()
【解析】試題分析:(Ⅰ)要證明線線垂直,一般用到線面垂直的性質(zhì)定理,即先要證線面垂直,首先由已知![]() 底面
底面![]() .知
.知![]() ,因此要證
,因此要證![]() 平面
平面![]() ,從而只要證
,從而只要證![]() ,這在
,這在![]() 中可證;(Ⅱ)要求點(diǎn)到平面的距離,可過點(diǎn)作平面的垂線,由(Ⅰ)的證明,可得
中可證;(Ⅱ)要求點(diǎn)到平面的距離,可過點(diǎn)作平面的垂線,由(Ⅰ)的證明,可得![]() 平面
平面![]() ,從而有
,從而有![]() 平面
平面![]() ,因此平面
,因此平面![]() 平面
平面![]() ,因此只要過
,因此只要過![]() 作
作![]() 于
于![]() ,則
,則![]() 就是的要作的垂線,線段
就是的要作的垂線,線段![]() 的長(zhǎng)就是所要求的距離.
的長(zhǎng)就是所要求的距離.
試題解析:(Ⅰ)證明:因?yàn)?/span>![]() ,
, ![]() ,
,
由余弦定理得![]() .
.
從而![]() ,∴
,∴![]() ,
,
又由![]() 底面
底面![]() ,
, ![]() 面
面![]() ,可得
,可得![]() .
.
所以![]() 平面
平面![]() .故
.故![]() .
.
(Ⅱ)解:作![]() ,垂足為
,垂足為![]() .
.
已知![]() 底面
底面![]() ,則
,則![]() ,
,
由(Ⅰ)知![]() ,又
,又![]() ,所以
,所以![]() .
.
故![]() 平面
平面![]() ,
, ![]() .
.
則![]() 平面
平面![]() .
.
由題設(shè)知, ![]() ,則
,則![]() ,
, ![]() ,
,
根據(jù)![]() ,得
,得![]() ,
,
即點(diǎn)![]() 到面
到面![]() 的距離為
的距離為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線l1經(jīng)過兩點(diǎn)(-1,-2),(-1,4),直線l2經(jīng)過兩點(diǎn)(2,1),(6,y),且l1⊥l2,則y=( )
A. -2 B. 1 C. 2 D. 4
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() ,過其焦點(diǎn)
,過其焦點(diǎn)![]() 作兩條相互垂直且不平行于坐標(biāo)軸的直線,它們分別交拋物線
作兩條相互垂直且不平行于坐標(biāo)軸的直線,它們分別交拋物線![]() 于點(diǎn)
于點(diǎn)![]() 、
、![]() 和點(diǎn)
和點(diǎn)![]() 、
、![]() ,線段
,線段![]() 、
、![]() 的中點(diǎn)分別為
的中點(diǎn)分別為![]() 、
、![]() .
.
(Ⅰ)求線段![]() 的中點(diǎn)
的中點(diǎn)![]() 的軌跡方程;
的軌跡方程;
(Ⅱ)求![]() 面積的最小值;
面積的最小值;
(Ⅲ)過![]() 、
、![]() 的直線
的直線![]() 是否過定點(diǎn)?若是,求出定點(diǎn)坐標(biāo),若不是,請(qǐng)說明理由.
是否過定點(diǎn)?若是,求出定點(diǎn)坐標(biāo),若不是,請(qǐng)說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某班50位學(xué)生在2016年中考中的數(shù)學(xué)成績(jī)的頻率分布直方圖如圖所示,其中成績(jī)分組區(qū)間是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
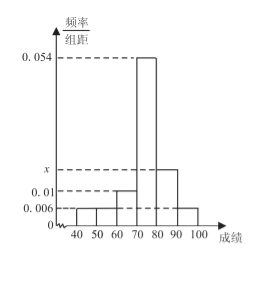
(Ⅰ)求圖中![]() 的值;
的值;
(Ⅱ)從成績(jī)不低于80分的學(xué)生中隨機(jī)選取2人,這2人中成績(jī)?cè)?0分以上(含90分)的人數(shù)記為![]() ,求
,求![]() 的數(shù)學(xué)期望.
的數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=2msin x-2cos2x+![]() -4m+3,且函數(shù)f(x)的最小值為19,求m的值.
-4m+3,且函數(shù)f(x)的最小值為19,求m的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某租賃公司擁有汽車100輛.當(dāng)每輛車的月租金為3 000元時(shí),可全部租出.當(dāng)每輛車的月租金每增加50元時(shí),未租出的車將會(huì)增加一輛.租出的車每輛每月需要維護(hù)費(fèi)150元,未租出的車每輛每月需要維護(hù)費(fèi)50元.
(1)當(dāng)每輛車的月租金定為3 600元時(shí),能租出多少輛車?
(2)當(dāng)每輛車的月租金定為多少元時(shí),租賃公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在邊長(zhǎng)為![]() 的菱形
的菱形![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 分別是邊
分別是邊![]() ,
,![]() 的中點(diǎn),
的中點(diǎn),![]() ,沿
,沿![]() 將
將![]() 翻折到
翻折到![]() ,連接
,連接![]() ,得到如圖的五棱錐
,得到如圖的五棱錐![]() ,且
,且![]() .
.
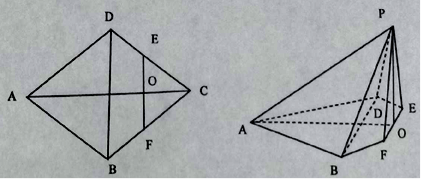
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com