
【題目】已知函數![]()
(1)當![]() 的極值;
的極值;
(2)若函數![]() 在[1,3]上是減函數,求實數a的取值范圍.
在[1,3]上是減函數,求實數a的取值范圍.
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左焦點為
的左焦點為![]() ,短軸的兩個端點分別為A,B,且滿足:
,短軸的兩個端點分別為A,B,且滿足:![]() ,且橢圓經過點
,且橢圓經過點![]()
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設過點M![]() 的動直線
的動直線![]() (與X軸不重合)與橢圓C相交于P,Q兩點,在X軸上是否存在一定點T,無論直線
(與X軸不重合)與橢圓C相交于P,Q兩點,在X軸上是否存在一定點T,無論直線![]() 如何轉動,點T始終在以PQ為直徑的圓上?若有,求點T的坐標,若無,說明理由。
如何轉動,點T始終在以PQ為直徑的圓上?若有,求點T的坐標,若無,說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+(x-1)|x-a|.
(1)若a=-1,解方程f(x)=1;
(2)若函數f(x)在R上單調遞增,求實數a的取值范圍;
(3)是否存在實數a,使不等式f(x)≥2x-3對任意x∈R恒成立?若存在,求出a的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為調查人們在購物時的支付習慣,某超市對隨機抽取的600名顧客的支付方式進行了統計,數據如下表所示:
支付方式 | 微信 | 支付寶 | 購物卡 | 現金 |
人數 | 200 | 150 | 150 | 100 |
現有甲、乙、丙三人將進入該超市購物,各人支付方式相互獨立,假設以頻率近似代替概率.
(1)求三人中使用微信支付的人數多于現金支付人數的概率;
(2)記![]() 為三人中使用支付寶支付的人數,求
為三人中使用支付寶支付的人數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】汽車的“燃油效率”是指汽車每消耗1升汽油行駛的里程,下圖描述了甲、乙、丙三輛汽車在不同速度下的燃油效率情況. 下列敘述中正確的是( )

A. 消耗1升汽油,乙車最多可行駛5千米
B. 以相同速度行駛相同路程,三輛車中,甲車消耗汽油最多
C. 甲車以80千米/小時的速度行駛1小時,消耗10升汽油
D. 某城市機動車最高限速80千米/小時. 相同條件下,在該市用丙車比用乙車更省油
查看答案和解析>>
科目:高中數學 來源: 題型:
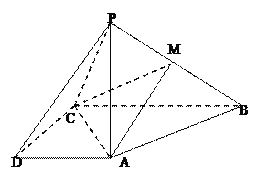
【題目】如圖,在四棱錐![]() 中,PA⊥底面ABCD,AD||BC,AD⊥CD,BC=2,AD=CD=1,M是PB的中點.
中,PA⊥底面ABCD,AD||BC,AD⊥CD,BC=2,AD=CD=1,M是PB的中點.
(1)求證:AM||平面PCD;
(2)求證:平面ACM⊥平面PAB;
(3)若PC與平面ACM所成角為30°,求PA的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com