【題目】乒乓球單打比賽在甲、乙兩名運動員間進行，比賽采用7局4勝制（即先勝4局者獲勝，比賽結束），假設兩人在每一局比賽中獲勝的可能性相同．
（1）求乙以4比1獲勝的概率；
（2）求甲獲勝且比賽局數多于5局的概率．
【答案】（1）
（2）
【解析】
（1）記“乙以4比1獲勝”為事件A ，，則A表示乙贏了3局甲贏了1局，且第五局乙贏，再根據n次獨立重復實驗中恰好發生k次的概率計算公式求得
的值。（2）利用n次獨立重復實驗中恰好發生k次的概率計算公式求得甲以4比2獲勝的概率，以及甲以4比3獲勝的概率，再把這2個概率值相加，即得所求。
解：（1）由已知，甲、乙兩名運動員在每一局比賽中獲勝的概率都是
，
記“乙以4比1獲勝”為事件A，則A表示乙贏了3局甲贏了一局，且第五局乙贏，
∴
．
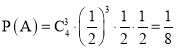（2）記“甲獲勝且比賽局數多于5局”為事件B，則B表示甲以4比2獲勝，或甲以4比3獲勝．
因為甲以4比2獲勝，表示前5局比賽中甲贏了3局且第六局比賽中甲贏了，
這時，無需進行第7局比賽，故甲以4比2獲勝的概率為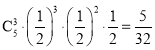
．
甲以4比3獲勝，表示前6局比賽中甲贏了3局且第7局比賽中甲贏了，
故甲以4比3獲勝的概率為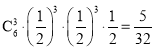
，
故甲獲勝且比賽局數多于5局的概率為
．
名師金手指領銜課時系列答案科目：高中數學 來源： 題型：
【題目】將圓
上每一點的橫坐標變為原來的2倍，縱坐標變為原來的4倍，得曲線
.
（1）寫出的參數方程；
（2）設直線
與的交點為
，以坐標原點為極點，
軸正半軸為極軸建立極坐標系，求過線段
的中點與
垂直的直線的極坐標方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設f（x）＝|lnx|，若函數g（x）＝f（x）-ax在區間（0，4）上有三個零點，則實數a的取值范圍是（ ）
A. （0，
）B. （
，e）C. （，）D. （0，）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出如下四個命題：①若“
且
”為假命題，則
均為假命題；②命題“若
，則
”的否命題為“若
，則
”； ③“
，則
”的否定是“
，則
”；④在
中，“
”是“
”的充要條件．其中正確的命題的個數是（ ）
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從甲地到乙地要經過3個十字路口，設各路口信號燈工作相互獨立，且在各路口遇到紅燈的概率分別為
.
（Ⅰ）設
表示一輛車從甲地到乙地遇到紅燈的個數，求隨機變量
的分布列和數學期望；
（Ⅱ）若有2輛車獨立地從甲地到乙地，求這2輛車共遇到1個紅燈的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于定義域為
的函數
，如果存在區間
，同時滿足：①函數在區間內是單調函數；②當定義域為
時，
的值域也是，則稱是該函數的和諧區間.
（1）求證：函數
不存在和諧區間；
（2）已知：函數
有和諧區間，當
變化時，求出
的最大值；
（3）易知，函數
是以任一區間為它的“和諧區間”，試再舉一例有和諧區間的函數，并寫出它的個和諧區間（不需要證明，但是不能用本題已經討論過的以及形如
的函數）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為迎接中國共產黨的十九大的到來，某校舉辦了“祖國，你好”的詩歌朗誦比賽.該校高三年級準備從包括甲、乙、丙在內的7名學生中選派4名學生參加，要求甲、乙、丙這3名同學中至少有1人參加，且當這3名同學都參加時，甲和乙的朗誦順序不能相鄰，那么選派的4名學生不同的朗誦順序的種數為（ ）
A. 720 B. 768 C. 810 D. 816
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
