
【題目】設數列{an}的前n項和為Sn,且Sn=2an﹣2(n∈N*),數列{bn}滿足bn=(2n﹣1)an,數列{bn}的前n項和Tn(n∈N*),
(1)求數列{an}和{bn}的通項公式;
(2)求數列{bn}的前n項和Tn;
(3)求![]() 的最小值以及取得最小值時n的值.
的最小值以及取得最小值時n的值.
【答案】(1)an=(2n﹣1)2n (2)Tn=(2n﹣3)2n+1+6 (3)n=3時,最小值為16
【解析】
(1)當![]() 時,
時,![]() ,相減可得
,相減可得![]() ,利用等比數列的定義與通項公式,即可得出數列
,利用等比數列的定義與通項公式,即可得出數列![]() 的通項公式,進而可得
的通項公式,進而可得![]() 的通項公式;(2)利用錯位相減法,結合等比數列的求和公式,即可得出數列
的通項公式;(2)利用錯位相減法,結合等比數列的求和公式,即可得出數列![]() 的前
的前![]() 項和
項和![]() ;(3)利用(2)可得
;(3)利用(2)可得![]()
![]() ,根據基本不等式的性質即可得結果.
,根據基本不等式的性質即可得結果.
(1)當n=1時,S1=2a1﹣2,所以a1=2.
當n≥2時,Sn=2an﹣2, Sn﹣1=2an﹣1﹣2,
兩式相減可得,
an=2an﹣2an﹣1,an=2an﹣1,
∴{an}為首項為2,公比為2的等比數列,
∴an=2n
bn=(2n﹣1)2n.
(2)因為Tn=121+322+523+…+(2n﹣3)2n﹣1+(2n﹣1)2n;①
所以2Tn=122+323+…+(2n﹣5)2n﹣1+(2n﹣3)2n+(2n﹣1)2n+1;②
由①﹣②得﹣Tn=2+23+24+…+2n+1﹣(2n﹣1)2n+1,
化簡得Tn=(2n﹣3)2n+1+6.
(3)![]() =4n﹣6+
=4n﹣6+![]()
![]() ,
,
當![]() ,即n=3時,最小值為16.
,即n=3時,最小值為16.


 全優沖刺100分系列答案
全優沖刺100分系列答案 英才點津系列答案
英才點津系列答案 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的一個最高點為
的一個最高點為![]() ,與點
,與點![]() 相鄰一個最低點為
相鄰一個最低點為![]() ,直線
,直線![]() 與
與![]() 軸的交點為
軸的交點為![]() .
.
(1)求函數![]() 的解析式;
的解析式;
(2)求函數![]() 的單調增區間;
的單調增區間;
(3)若![]() 時,函數
時,函數![]() 恰有一個零點,求實數
恰有一個零點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據調查,某地區有300萬從事傳統農業的農民,人均年收入6000元,為了增加農民的收入,當地政府積極引進資本,建立各種加工企業,對當地的農產品進行深加工,同時吸收當地部分農民進入加工企業工作,據估計,如果有![]() 萬人進企業工作,那么剩下從事傳統農業的農民的人均年收入有望提高
萬人進企業工作,那么剩下從事傳統農業的農民的人均年收入有望提高![]() ,而進入企業工作的農民的人均年收入為
,而進入企業工作的農民的人均年收入為![]() 元.
元.
(1)在建立加工企業后,多少農民進入企業工作,能夠使剩下從事傳統農業農民的總收入最大,并求出最大值;
(2)為了保證傳統農業的順利進行,限制農民加入加工企業的人數不能超過總人數的![]() ,當地政府如何引導農民,即
,當地政府如何引導農民,即![]() 取何值時,能使300萬農民的年總收入最大.
取何值時,能使300萬農民的年總收入最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 的圖象上存在關于直線
的圖象上存在關于直線![]() 對稱的不同兩點,則稱
對稱的不同兩點,則稱![]() 具有性質
具有性質![]() .已知
.已知![]() 為常數,函數
為常數,函數![]() ,
,![]() ,對于命題:①存在
,對于命題:①存在![]() ,使得
,使得![]() 具有性質
具有性質![]() ;②存在
;②存在![]() ,使得
,使得![]() 具有性質
具有性質![]() ,下列判斷正確的是( )
,下列判斷正確的是( )
A.①和②均為真命題B.①和②均是假命題
C.①是真命題,②是假命題D.①是假命題,②是真命題
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() 的定義域分別為
的定義域分別為![]() ,若存在常數
,若存在常數![]() ,滿足:①對任意
,滿足:①對任意![]() ,恒有
,恒有![]() ,且
,且![]() .②對任意
.②對任意![]() ,關于
,關于![]() 的不等式組
的不等式組![]()
![]() 恒有解,則稱
恒有解,則稱![]() 為
為![]() 的一個“
的一個“![]() 型函數”.
型函數”.
(1)設函數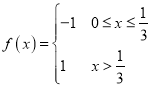 和
和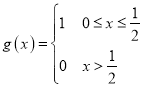 ,求證:
,求證:![]() 為
為![]() 的一個“
的一個“![]() 型函數”;
型函數”;
(2)設常數![]() ,函數
,函數![]() ,
,![]() .若
.若![]() 為
為![]() 的一個“
的一個“![]() 型函數”,求
型函數”,求![]() 的取值范圍;
的取值范圍;
(3)設函數![]() .問:是否存在常數
.問:是否存在常數![]() ,使得函數
,使得函數![]() 為
為![]() 的一個“
的一個“![]() 型函數”?若存在,求
型函數”?若存在,求![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某學校高三年級共800名男生中隨機抽取50名學生作為樣本測量身高.測量發現被測學生身高全部介于155cm和195cm之間,將測量結果按如下方式分成八組:第一組![]() ;第二組
;第二組![]() ;…;第八組
;…;第八組![]() .下圖是按上述分組方法得到的頻率分布直方圖的一部分.已知第一組與第八組人數相同,第六組與第八組人數之和為第七組的兩倍.
.下圖是按上述分組方法得到的頻率分布直方圖的一部分.已知第一組與第八組人數相同,第六組與第八組人數之和為第七組的兩倍.
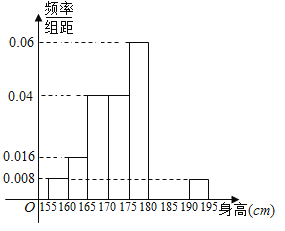
(1)估計這所學校高三年級全體男生身高在180cm以上(含180cm)的人數;
(2)求第六組和第七組的頻率并補充完整頻率分布直方圖.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2012年,在“雜交水稻之父”袁隆平的實驗田內種植了![]() ,
,![]() 兩個品種的水稻,為了篩選出更優的品種,在
兩個品種的水稻,為了篩選出更優的品種,在![]() ,
,![]() 兩個品種的實驗田中分別抽取7塊實驗田,如圖所示的莖葉圖記錄了這14塊實驗田的畝產量(單位:
兩個品種的實驗田中分別抽取7塊實驗田,如圖所示的莖葉圖記錄了這14塊實驗田的畝產量(單位:![]() ),通過莖葉圖比較兩個品種的均值及方差,并從中挑選一個品種進行以后的推廣,有如下結論:①
),通過莖葉圖比較兩個品種的均值及方差,并從中挑選一個品種進行以后的推廣,有如下結論:①![]() 品種水稻的平均產量高于
品種水稻的平均產量高于![]() 品種水稻,推廣
品種水稻,推廣![]() 品種水稻;②
品種水稻;②![]() 品種水稻的平均產量高于
品種水稻的平均產量高于![]() 品種水稻,推廣
品種水稻,推廣![]() 品種水稻;③
品種水稻;③![]() 品種水稻比
品種水稻比![]() 品種水稻產量更穩定,推廣
品種水稻產量更穩定,推廣![]() 品種水稻;④
品種水稻;④![]() 品種水稻比
品種水稻比![]() 品種水稻產量更穩定,推廣
品種水稻產量更穩定,推廣![]() 品種水稻;其中正確結論的編號為( )
品種水稻;其中正確結論的編號為( )

A.①②B.①③C.②④D.①④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com