
 (本題滿分14分)已知如圖,橢圓方程為
(本題滿分14分)已知如圖,橢圓方程為![]()
![]() .P為橢圓上的動點,
.P為橢圓上的動點,
F1、F2為橢圓的兩焦點,當點P不在x軸上時,過F1作∠F1PF2的外角
平分線的垂線F1M,垂足為M,當點P在x軸上時,定義M與P重合.
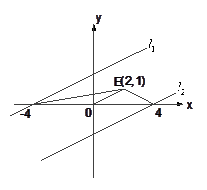
(1)求M點的軌跡T的方程;(2)已知![]() 、
、![]() ,
,
試探究是否存在這樣的點![]() :
:![]() 是軌跡T內部的整點
是軌跡T內部的整點
(平面內橫、縱坐標均為整數的點稱為整點),且△OEQ的面積![]() ?
?
若存在,求出點Q的坐標,若不存在,說明理由.
(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
![]()
(1)當點P不在x軸上時,延長F1M與F2P的延長線相交
于點N,連結OM,∵![]() ,
,![]()
∴![]() ≌
≌![]() ∴M是線段
∴M是線段![]() 的中點,
的中點,![]() |----------2分
|----------2分
∴ ![]() =
=![]()
![]() =
=![]() =
=![]()
∵點P在橢圓上∴![]() =
=![]() ∴
∴![]() =4,----------------------4分
=4,----------------------4分
當點P在x軸上時,M與P重合
 ∴M點的軌跡T的方程為:
∴M點的軌跡T的方程為:![]() .----------------------6分
.----------------------6分
(2)連結OE,易知軌跡T上有兩個點
A![]() ,B
,B![]() 滿足
滿足![]() ,
,
分別過A、B作直線OE的兩條平行線![]() 、
、![]() .
.
∵同底等高的兩個三角形的面積相等
∴符合條件的點均在直線![]() 、
、![]() 上.------ ----------7分
上.------ ----------7分
∵![]() ∴直線
∴直線![]() 、
、![]() 的方程分別為:
的方程分別為:![]() 、
、![]() -------------------8分
-------------------8分
設點![]() (
(![]() )∵
)∵![]() 在軌跡T內,∴
在軌跡T內,∴![]() --------------------------------9分
--------------------------------9分
分別解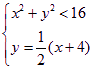 與
與 得
得![]() 與
與![]() -------11分
-------11分
∵![]() ∴
∴![]() 為偶數,在
為偶數,在![]() 上
上![]() 對應的
對應的![]()
在![]() 上
上![]() ,對應的
,對應的![]() -----------13分
-----------13分
∴滿足條件的點![]() 存在,共有6個,它們的坐標分別為:
存在,共有6個,它們的坐標分別為:
![]()
![]() .------------14分
.------------14分


科目:高中數學 來源:2012-2013學年吉林省高三第一次月考文科數學試卷(解析版) 題型:解答題
(本題滿分14分)已知函數
(1)若 ,求x的值;
,求x的值;
(2)若 對于
對于 恒成立,求實數m的取值范圍.
恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省惠州市高三第三次調研考試數學理卷 題型:解答題
(本題滿分14分)
已知橢圓 :
: 的離心率為
的離心率為 ,過坐標原點
,過坐標原點 且斜率為
且斜率為 的直線
的直線 與
與 相交于
相交于 、
、 ,
, .
.
⑴求 、
、 的值;
的值;
⑵若動圓 與橢圓
與橢圓 和直線
和直線 都沒有公共點,試求
都沒有公共點,試求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省惠州市高三第三次調研考試數學理卷 題型:解答題
((本題滿分14分)
已知梯形ABCD中,AD∥BC,∠ABC =∠BAD = ,AB=BC=2AD=4,E、F分別是AB、CD上的點,EF∥BC,AE = x,G是BC的中點.沿EF將梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如圖).
,AB=BC=2AD=4,E、F分別是AB、CD上的點,EF∥BC,AE = x,G是BC的中點.沿EF將梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如圖).
(1)當x=2時,求證:BD⊥EG ;
(2)若以F、B、C、D為頂點的三棱錐的體積記為 ,
,
求 的最大值;
的最大值;


(3)當 取得最大值時,求二面角D-BF-C的余弦值.
取得最大值時,求二面角D-BF-C的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com