
【題目】已知集合![]() .
.
(1)若![]() 是
是![]() 的充分條件,求
的充分條件,求![]() 的取值范圍.
的取值范圍.
(2)若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
求解二次不等式化簡集合![]() .(1)對
.(1)對![]() 分類求解集合
分類求解集合![]() ,然后把
,然后把![]() 是
是![]() 的充分條件轉(zhuǎn)化為含有
的充分條件轉(zhuǎn)化為含有![]() 的不等式組,即可求解
的不等式組,即可求解![]() 的范圍;(2)由
的范圍;(2)由![]() ,借助于集合
,借助于集合![]() ,
,![]() 的端點值間的關系列不等式求解
的端點值間的關系列不等式求解![]() 的范圍.
的范圍.
A={x|x2-6x+8<0}={x|2<x<4},
B={x|(x-a)(x-3a)<0}.
(1)當a=0時,B=,不合題意.
當a>0時,B={x|a<x<3a},要滿足題意,
則![]() ,解得
,解得![]() ≤a≤2.
≤a≤2.
當a<0時,B={x|3a<x<a},要滿足題意,
則![]() ,無解.
,無解.
綜上,a的取值范圍為![]() .
.
(2)要滿足A∩B=,
當a>0時,B={x|a<x<3a}
則a≥4或3a≤2,即0<a≤![]() 或a≥4.
或a≥4.
當a<0時,B={x|3a<x<a},
則a≤2或a≥![]() ,即a<0.
,即a<0.
當a=0時,B=,A∩B=.
綜上,a的取值范圍為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】有一個同學家開了一個奶茶店,他為了研究氣溫對熱奶茶銷售杯數(shù)的影響,從一季度中隨機選取5天,統(tǒng)計出氣溫與熱奶茶銷售杯數(shù),如表:
氣溫 | 0 | 4 | 12 | 19 | 27 |
熱奶茶銷售杯數(shù) | 150 | 132 | 130 | 104 | 94 |
(Ⅰ)求熱奶茶銷售杯數(shù)關于氣溫的線性回歸方程![]() (
(![]() 精確到0.1),若某天的氣溫為15oC,預測這天熱奶茶的銷售杯數(shù);
精確到0.1),若某天的氣溫為15oC,預測這天熱奶茶的銷售杯數(shù);
(Ⅱ)從表中的5天中任取一天,若已知所選取該天的熱奶茶銷售杯數(shù)大于120,求所選取該天熱奶茶銷售杯數(shù)大于130的概率.
參考數(shù)據(jù):![]() ,
,![]() .參考公式:
.參考公式: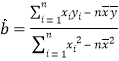 ,
,![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知拋物線![]() ,過焦點F的直線l與拋物線分別交于A、B兩點,O為坐標原點,且
,過焦點F的直線l與拋物線分別交于A、B兩點,O為坐標原點,且![]() .
.
(1)求拋物線的標準方程;
(2)對于拋物線上任一點Q,點P(2t,0)都滿足|PQ|≥2|t|,求實數(shù)t的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知點A(x1,y1),D(x2,y2)其中(x1<x2)是曲線y2=9x(y≥0).上的兩點,A,D兩點在x軸上的射影分別為點B,C且|BC|=3.
(Ⅰ)當點B的坐標為(1,0)時,求直線AD的方程:
(Ⅱ)記△AOD的面積為S1,梯形ABCD的面積為S2,求![]() 的范圍
的范圍
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知一列非零向量![]() 滿足:
滿足:![]() ,
,![]() ,其中
,其中![]() 是正數(shù)
是正數(shù)
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)求證:當![]() 時,向量
時,向量![]() 與
與![]() 的夾角為定值;
的夾角為定值;
(3)當![]() 時,把
時,把![]() 中所有與
中所有與![]() 共線的向量按原來的順序排成一列,記為
共線的向量按原來的順序排成一列,記為![]() ,令
,令![]() ,
,![]() 為坐標原點,求點列
為坐標原點,求點列![]() 的極限點
的極限點![]() 的坐標.(注:若點坐標為
的坐標.(注:若點坐標為![]() ,且
,且![]() ,則稱點
,則稱點![]() 為點列的極限點)
為點列的極限點)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() ,
, ![]() ,其中
,其中![]() 是自然常數(shù),
是自然常數(shù), ![]() .
.
(1)當![]() 時,求
時,求![]() 的極值,并證明
的極值,并證明![]() 恒成立;
恒成立;
(2)是否存在實數(shù)![]() ,使
,使![]() 的最小值為
的最小值為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某中藥種植基地有兩處種植區(qū)的藥材需在下周一、下周二兩天內(nèi)采摘完畢,基地員工一天可以完成一處種植區(qū)的采摘.由于下雨會影響藥材品質(zhì),基地收益如下表所示:
周一 | 無雨 | 無雨 | 有雨 | 有雨 |
周二 | 無雨 | 有雨 | 無雨 | 有雨 |
收益 |
|
|
|
|
若基地額外聘請工人,可在周一當天完成全部采摘任務.無雨時收益為![]() 萬元;有雨時,收益為
萬元;有雨時,收益為![]() 萬元.額外聘請工人的成本為
萬元.額外聘請工人的成本為![]() 萬元.
萬元.
已知下周一和下周二有雨的概率相同,兩天是否下雨互不影響,基地收益為![]() 萬元的概率為
萬元的概率為![]() .
.
(Ⅰ)若不額外聘請工人,寫出基地收益![]() 的分布列及基地的預期收益;
的分布列及基地的預期收益;
(Ⅱ)該基地是否應該外聘工人,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】定義函數(shù)![]() ,
,![]() (0,
(0,![]() )為
)為![]() 型函數(shù),共中
型函數(shù),共中![]() .
.
(1)若![]() 是
是![]() 型函數(shù),求函數(shù)
型函數(shù),求函數(shù)![]() 的值域;
的值域;
(2)若![]() 是
是![]() 型函數(shù),求函數(shù)
型函數(shù),求函數(shù)![]() 極值點個數(shù);
極值點個數(shù);
(3)若![]() 是
是![]() 型函數(shù),在
型函數(shù),在![]() 上有三點A、B、C橫坐標分別為
上有三點A、B、C橫坐標分別為![]() 、
、![]() 、
、![]() ,其中
,其中![]() <
<![]() <
<![]() ,試判斷直線AB的斜率與直線BC的斜率的大小并說明理由.
,試判斷直線AB的斜率與直線BC的斜率的大小并說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,將一塊直角三角形木板![]() 置于平面直角坐標系中,已知
置于平面直角坐標系中,已知![]() ,點
,點![]() 是三角形木板內(nèi)一點,現(xiàn)因三角形木板中陰影部分受到損壞,要把損壞部分鋸掉,可用經(jīng)過點
是三角形木板內(nèi)一點,現(xiàn)因三角形木板中陰影部分受到損壞,要把損壞部分鋸掉,可用經(jīng)過點![]() 的任一直線
的任一直線![]() 將三角形木板鋸成
將三角形木板鋸成![]() .設直線
.設直線![]() 的斜率為
的斜率為![]() .
.
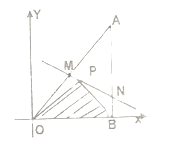
(Ⅰ)求點![]() 的坐標及直線
的坐標及直線![]() 的斜率
的斜率![]() 的范圍;
的范圍;
(Ⅱ)令![]() 的面積為
的面積為![]() ,試求出
,試求出![]() 的取值范圍;
的取值范圍;
(Ⅲ)令(Ⅱ)中![]() 的取值范圍為集合
的取值范圍為集合![]() ,若
,若![]() 對
對![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com