
【題目】已知函數![]() .
.
(1)討論函數![]() 的單調區間;
的單調區間;
(2)若![]() ,
, ![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)
(2)![]()
【解析】試題分析:(1) 求出函數的導數,通過討論![]() 的范圍,
的范圍, ![]() 得增區間,
得增區間, ![]() 得減區間; (2)問題轉化為
得減區間; (2)問題轉化為![]() ,討論
,討論![]() 的范圍,根據函數的單調性求出
的范圍,根據函數的單調性求出![]() 的最小值即可求出
的最小值即可求出![]() 的范圍.
的范圍.
試題解析:(1)![]() .
.
(i)當![]() 時,
時, ![]() ,函數
,函數![]() 在
在![]() 上單調遞增;
上單調遞增;
(ii)當![]() 時,令
時,令![]() ,則
,則![]() ,
,
當![]() ,即
,即![]() ,函數
,函數![]() 單調遞增;
單調遞增;
當![]() ,即
,即![]() 時,函數
時,函數![]() 單調遞減.
單調遞減.
綜上,當![]() 時,函數
時,函數![]() 在
在![]() 上單調遞增;當
上單調遞增;當![]() 時,函數
時,函數![]() 的單調遞增區間是
的單調遞增區間是![]() ,單調遞減區間是
,單調遞減區間是![]() .
.
(2)令![]() ,由(1)可知,函數
,由(1)可知,函數![]() 的最小值為
的最小值為![]() ,所以
,所以![]() ,即
,即![]() .
.
![]() 恒成立與
恒成立與![]() 恒成立等價,
恒成立等價,
令![]() ,即
,即![]() ,則
,則![]() .
.
①當![]() 時,
時, ![]() .(或令
.(或令![]() ,則
,則
![]() 在
在![]() 上遞增,∴
上遞增,∴![]() ,∴
,∴![]() 在
在![]() 上遞增,∴
上遞增,∴![]() .
.
∴![]() ).
).
∴![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
∴![]() ,
,
∴![]() 恒成立.
恒成立.
②當![]() 時,令
時,令![]() ,則
,則![]() ,
,
當![]() 時,
時, ![]() ,函數
,函數![]() 單調遞增.
單調遞增.
又![]() ,
, ![]() ,
,
∴存在![]() ,使得
,使得![]() ,故當
,故當![]() 時,
時, ![]() ,即
,即![]() ,故函數
,故函數![]() 在
在![]() 上單調遞減;當
上單調遞減;當![]() 時,
時, ![]() ,即
,即![]() ,故函數
,故函數![]() 在
在![]() 上單調遞增,
上單調遞增,
∴![]() ,
,
即![]() ,
, ![]() 不恒成立,
不恒成立,
綜上所述, ![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】在遂寧市中央商務區的街道,有一中年人吆喝“送錢”,只見他手拿一黑色小布袋,袋中有3只黃色、2只白色的乒乓球(其體積,質地完全相同),旁邊立著一塊小黑板寫道:
摸球方法:從袋中隨機摸出3個球,若摸得統一顏色的3個球,攤主送個摸球者10元錢;若摸得非同一顏色的3個球。摸球者付給攤主2元錢。
(1)摸出的3個球中至少有1個白球的概率是多少?
(2)假定一天中有100人次摸獎,試從概率的角度估算一下這個攤主一個月(按30天計)能賺多少錢?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l經過點![]() ,則
,則
(1)若直線l與x軸、y軸的正半軸分別交于A、B兩點,且△OAB的面積為4,求直線l的方程;
(2)若直線l與原點距離為2,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設各項均為正數的數列![]() 的前n項和為
的前n項和為![]() ,滿足
,滿足![]() ,且
,且![]() ,公比大于1的等比數列
,公比大于1的等比數列![]() 滿足
滿足![]() ,
, ![]() .
.
(1)求證數列![]() 是等差數列,并求其通項公式;
是等差數列,并求其通項公式;
(2)若![]() ,求數列
,求數列![]() 的前n項和
的前n項和![]() ;
;
(3)在(2)的條件下,若![]() 對一切正整數n恒成立,求實數t的取值范圍.
對一切正整數n恒成立,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和Sn滿足![]() ,
,
(1)求數列{an}的通項公式;
(2)求證:數列{an}中的任意三項不可能成等差數列;
(3)設![]() ,Tn為{bn}的前n項和,求證
,Tn為{bn}的前n項和,求證![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了在夏季降溫和冬季供暖時減少能源損耗,房屋的屋頂和外墻需要建造隔熱層,某幢建筑物要建造可使用20年的隔熱層,每厘米厚的隔熱層建造成本為6萬元,該建筑物每年的能源消耗費用C(單位:萬元)與隔熱層厚度x(單位:cm)滿足關系:C(x)=![]() (0≤x≤10),若不建隔熱層,每年能源消耗費用為8萬元.設f(x)為隔熱層建造費用與20年的能源消耗費用之和.
(0≤x≤10),若不建隔熱層,每年能源消耗費用為8萬元.設f(x)為隔熱層建造費用與20年的能源消耗費用之和.
(1)求k的值及f(x)的表達式;
(2)隔熱層修建多厚時,總費用f(x)達到最小,并求最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的定義域為[-1,5],部分對應值如下表,
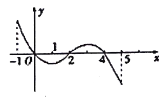
的定義域為[-1,5],部分對應值如下表,![]() 的導函數
的導函數![]() 的圖象如圖所示,下列關于
的圖象如圖所示,下列關于![]() 的命題:
的命題:
| -1 | 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
①函數![]() 的極大值點為0,4;
的極大值點為0,4;
②函數![]() 在[0,2]上是減函數;
在[0,2]上是減函數;
③如果當![]() 時,
時,![]() 的最大值是2,那么
的最大值是2,那么![]() 的最大值為4;
的最大值為4;
④當![]() 時,函數
時,函數![]() 有4個零點.
有4個零點.
其中正確命題的序號是__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com