
【題目】已知橢圓![]() :
: ![]() (
(![]() )的上、下兩個焦點分別為
)的上、下兩個焦點分別為![]() ,
, ![]() ,過
,過![]() 的直線交橢圓于
的直線交橢圓于![]() ,
, ![]() 兩點,且
兩點,且![]() 的周長為8,橢圓
的周長為8,橢圓![]() 的離心率為
的離心率為![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)已知![]() 為坐標(biāo)原點,直線
為坐標(biāo)原點,直線![]() :
: ![]() 與橢圓
與橢圓![]() 有且僅有一個公共點,點
有且僅有一個公共點,點![]() ,
, ![]() 是直線
是直線![]() 上的兩點,且
上的兩點,且![]() ,
, ![]() ,求四邊形
,求四邊形![]() 面積
面積![]() 的最大值.
的最大值.
【答案】(1)![]() .(2)4.
.(2)4.
【解析】試題分析:(1)首先根據(jù)橢圓中焦點三角形周長結(jié)論可得![]() ,,然后由
,,然后由![]() ,即可得橢圓的基本量求解方程(2)直線與橢圓只有一個交點,則聯(lián)立后方程
,即可得橢圓的基本量求解方程(2)直線與橢圓只有一個交點,則聯(lián)立后方程![]() =0得m,k的關(guān)系式,然后由點到直線距離公式得d1,d2,寫出四邊形
=0得m,k的關(guān)系式,然后由點到直線距離公式得d1,d2,寫出四邊形![]() 的面積
的面積![]() ,將各量代入化簡求解即可
,將各量代入化簡求解即可
試題解析:
(1)因為![]() 的周長為8,所以
的周長為8,所以![]() ,所以
,所以![]() .又因為
.又因為![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以橢圓![]() 的標(biāo)準(zhǔn)方程為
的標(biāo)準(zhǔn)方程為![]() .
.
(2)將直線![]() 的方程
的方程![]() 代入到橢圓方程
代入到橢圓方程![]() 中,得
中,得![]()
![]() .
.
由直線與橢圓僅有一個公共點,知![]()
![]() ,化簡得
,化簡得![]() .
.
設(shè)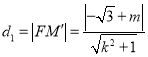 ,
, 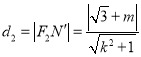 ,
,
所以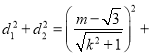
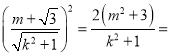
![]() ,
,
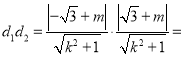
![]() ,
,
所以![]()
![]()
![]() .
.
因為四邊形![]() 的面積
的面積![]() ,
,
所以![]()
![]()
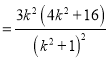 .
.
令![]() (
(![]() ),則
),則
![]()
![]()
![]()
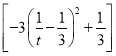 ,
,
所以當(dāng)![]() 時,
時, ![]() 取得最大值為16,故
取得最大值為16,故![]() ,即四邊形
,即四邊形![]() 面積的最大值為4.
面積的最大值為4.


科目:高中數(shù)學(xué) 來源: 題型:
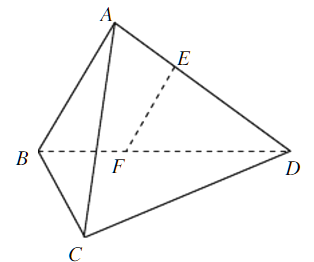
【題目】如圖,在三棱錐A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,點E、F(E與A、D不重合)分別在棱AD,BD上,且EF⊥AD.
求證:(1)EF∥平面ABC;
(2)AD⊥AC.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知雙曲線C的焦點與橢圓 ![]() =1的焦點相同,且漸近線方程為y=±
=1的焦點相同,且漸近線方程為y=± ![]() x.
x.
(1)求雙曲線C的標(biāo)準(zhǔn)方程;
(2)設(shè)F1為雙曲線的左焦點,P為雙曲線C的右支上一點,且線段PF1的中點在y軸上,求△PF1F2的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)x,y滿足約束條件  ,若目標(biāo)函數(shù)z=ax+by(a>0,b>0)的最大值為6,求
,若目標(biāo)函數(shù)z=ax+by(a>0,b>0)的最大值為6,求 ![]() +
+ ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】不等式(x+ ![]() )(
)( ![]() ﹣x)≥0的解集是( )
﹣x)≥0的解集是( )
A.{x|﹣ ![]() ≤x≤
≤x≤ ![]() }
}
B.{x|x≤﹣ ![]() 或x≥
或x≥ ![]() }??
}??
C.{x|x<﹣ ![]() 或x>
或x> ![]() }
}
D.{x|﹣ ![]() <x<
<x< ![]() }
}
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ,
, ![]() ).
).
(1)如果曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(2)若![]() ,
, ![]() ,關(guān)于
,關(guān)于![]() 的不等式
的不等式![]() 的整數(shù)解有且只有一個,求
的整數(shù)解有且只有一個,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知 ![]() =(1,2),
=(1,2), ![]() =(﹣3,2),當(dāng)k為何值時:
=(﹣3,2),當(dāng)k為何值時:
(1)k ![]() +
+ ![]() 與
與 ![]() ﹣3
﹣3 ![]() 垂直;
垂直;
(2)k ![]() +
+ ![]() 與
與 ![]() ﹣3
﹣3 ![]() 平行,平行時它們是同向還是反向?
平行,平行時它們是同向還是反向?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分13分)
某電視臺播放甲、乙兩套連續(xù)劇,每次播放連續(xù)劇時,需要播放廣告.已知每次播放甲、乙兩套連續(xù)劇時,連續(xù)劇播放時長、廣告播放時長、收視人次如下表所示:
連續(xù)劇播放時長(分鐘) | 廣告播放時長(分鐘) | 收視人次(萬) | |
甲 | 70 | 5 | 60 |
乙 | 60 | 5 | 25 |
已知電視臺每周安排甲、乙連續(xù)劇的總播放時間不多于600分鐘,廣告的總播放時間不少于30分鐘,且甲連續(xù)劇播放的次數(shù)不多于乙連續(xù)劇播放次數(shù)的2倍.分別用![]() ,
,![]() 表示每周計劃播出的甲、乙兩套連續(xù)劇的次數(shù).
表示每周計劃播出的甲、乙兩套連續(xù)劇的次數(shù).
(I)用![]() ,
,![]() 列出滿足題目條件的數(shù)學(xué)關(guān)系式,并畫出相應(yīng)的平面區(qū)域;
列出滿足題目條件的數(shù)學(xué)關(guān)系式,并畫出相應(yīng)的平面區(qū)域;
(II)問電視臺每周播出甲、乙兩套連續(xù)劇各多少次,才能使收視人次最多?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】用簡單隨機抽樣方法從含有6個個體的總體中,抽取一個容量為2的樣本,某一個體a“第一次被抽到的概率”、“第二次被抽到的概率”、“在整個抽樣過程中被抽到”的概率分別是
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com