
【題目】已知橢圓![]() 的兩個焦點分別為
的兩個焦點分別為![]() ,
, ![]() ,離心率為
,離心率為![]() ,且過點
,且過點![]() .
.
(![]() )求橢圓
)求橢圓![]() 的標準方程.
的標準方程.
(![]() )
)![]() 、
、![]() 、
、![]() 、
、![]() 是橢圓
是橢圓![]() 上的四個不同的點,兩條都不和
上的四個不同的點,兩條都不和![]() 軸垂直的直線
軸垂直的直線![]() 和
和![]() 分別過點
分別過點![]() ,
, ![]() ,且這條直線互相垂直,求證:
,且這條直線互相垂直,求證: ![]() 為定值.
為定值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某興趣小組欲研究晝夜溫差大小與患感冒人數多少之間的關系,他們分別到氣象局與某醫院抄錄了![]() 至
至![]() 月份每月
月份每月![]() 號的晝夜溫差情況與因患感冒而就診的人數,得到如下資料:
號的晝夜溫差情況與因患感冒而就診的人數,得到如下資料:
日期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
晝夜溫差
|
|
|
|
|
|
|
就診人數 |
|
|
|
|
|
|
該興趣小組確定的研究方案是:先從這六組數據中選取![]() 組,用剩下的
組,用剩下的![]() 組數據求線性回歸方程,再用被選取的
組數據求線性回歸方程,再用被選取的![]() 組數據進行檢驗.
組數據進行檢驗.
(1)求選取的![]() 組數據恰好是相鄰兩月的概率;
組數據恰好是相鄰兩月的概率;
(2)若選取的是1月與![]() 月的兩組數據,請根據2至5月份的數據,求出
月的兩組數據,請根據2至5月份的數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過![]() 人,則認為得到的線性回歸方程是理想的,試問該小組所得線性回歸方程是否理想?
人,則認為得到的線性回歸方程是理想的,試問該小組所得線性回歸方程是否理想?
參考數據![]() ,
,![]()
(參考公式:
 ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
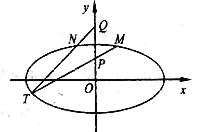
【題目】如圖,在平面直角坐標系![]() 中,橢圓
中,橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,以原點為圓心,橢圓
,以原點為圓心,橢圓![]() 的短半軸長為半徑的圓與直線
的短半軸長為半徑的圓與直線![]() 相切.
相切.
(1)求橢圓![]() 的方程;
的方程;
(2)已知點![]() ,設
,設![]() 是橢圓
是橢圓![]() 上關于
上關于![]() 軸對稱的不同兩點,直線
軸對稱的不同兩點,直線![]() 與
與![]() 相交于點
相交于點![]() ,求證:點
,求證:點![]() 在橢圓上.
在橢圓上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中正確的是__________.
①一個命題的逆命題為真,則它的逆否命題一定為真;
②“![]() ”是“
”是“![]() ”的充要條件;
”的充要條件;
③“![]() ,則
,則![]() ,
, ![]() 全為
全為![]() ” 的逆否命題是“若
” 的逆否命題是“若![]() ,
, ![]() 全不為
全不為![]() ,則
,則![]() ”
”
④一個命題的否命題為真,則它的逆命題一定為真;
⑤“![]() 為假命題”是“
為假命題”是“![]() 為真命題”的充分不必要條件.
為真命題”的充分不必要條件.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】網購已經成為一種時尚,商家為了鼓勵消費,購買時在店鋪領取優惠券,買后給予好評返還現金等促銷手段.經統計,近五年某店鋪用于促銷的費用![]() (萬元)與當年度該店鋪的銷售收人
(萬元)與當年度該店鋪的銷售收人![]() (萬元)的數據如下表:
(萬元)的數據如下表:
年份 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 |
促銷費用 |
|
|
|
|
|
銷售收入 |
|
|
|
|
|
(1)請根據上表提供的數據,用最小二乘法求出/span>![]() 關于
關于![]() 的線性回歸方
的線性回歸方![]() ;
;
(2)2018年度該店鋪預測銷售收人至少達到![]() 萬元,則該店鋪至少準備投入多少萬元的促銷費?
萬元,則該店鋪至少準備投入多少萬元的促銷費?
參考公式: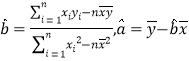
參考數據: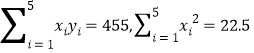
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() ,
,![]() 兩個小島相距
兩個小島相距![]() 海里,
海里,![]() 島在
島在![]() 島的正南方,現在甲船從
島的正南方,現在甲船從![]() 島出發,以
島出發,以![]() 海里/時的速度向
海里/時的速度向![]() 島行駛,而乙船同時以
島行駛,而乙船同時以![]() 海里/時的速度離開
海里/時的速度離開![]() 島向南偏東
島向南偏東![]() 方向行駛,行駛多少時間后,兩船相距最近?并求出兩船的最近距離.
方向行駛,行駛多少時間后,兩船相距最近?并求出兩船的最近距離.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知任意角
中,已知任意角![]() 以坐標原點
以坐標原點![]() 為頂點,
為頂點,![]() 軸的非負半軸為始邊,若終邊經過點
軸的非負半軸為始邊,若終邊經過點![]() ,且
,且![]() ,定義:
,定義:![]() ,稱“
,稱“![]() ”為“正余弦函數”,對于“正余弦函數
”為“正余弦函數”,對于“正余弦函數![]() ”,有同學得到以下性質:
”,有同學得到以下性質:
①該函數的值域為![]() ; ②該函數的圖象關于原點對稱;
; ②該函數的圖象關于原點對稱;
③該函數的圖象關于直線![]() 對稱; ④該函數為周期函數,且最小正周期為
對稱; ④該函數為周期函數,且最小正周期為![]() ;
;
⑤該函數的遞增區間為![]() .
.
其中正確的是__________.(填上所有正確性質的序號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com