【題目】已知雙曲線
：
的右焦點為
，半焦距
，點到右準線
的距離為
，過點作雙曲線的兩條互相垂直的弦
，
，設，的中點分別為
，
.
（1）求雙曲線的標準方程；
（2）證明：直線
必過定點，并求出此定點坐標.
【答案】（1）
（2）證明見解析；定點
【解析】
（1）由題意可得
的值，再由點
到直線
的距離為
，可得
的值，再由，
，之間的關系求出雙曲線的方程；
（2）設弦
所在的直線方程，與雙曲線的方程聯立可得兩根之和進而可得的中點
的坐標，再由橢圓可得弦
的中點
的坐標，分別討論當
的斜率存在和不存在兩種情況可得直線恒過定點.
（1）由題設可得
，
，所以
，
.
所以雙曲線的標準方程為.
（2）證明：點
，設過點的弦所在的直線方程為
，
，
，
則有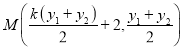
.
聯立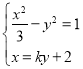
，可得
.
因為弦與雙曲線
有兩個交點，所以
，
所以
，所以
.
（1）當
時，點即是點，此時，直線為
軸.
（2）當
時，將上式點坐標中的
換成
，同理可得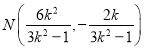
.
①當直線不垂直于軸時，
直線的斜率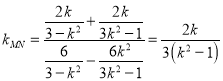
，
其方程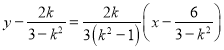
，化簡得
，
所以直線過定點；
②當直線垂直于軸時，
，此時，
，直線也過定點.
綜上所述，直線過定點.
奪冠金卷全能練考系列答案科目：高中數學 來源： 題型：
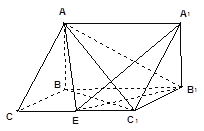
【題目】如圖，在三棱柱
中，已知
，
，
側面
.
（Ⅰ）求直線
與底面
所成角正切值；
（Ⅱ）在棱
（不包含端點）上確定一點E的位置，
使得
（要求說明理由）；
（Ⅲ）在（Ⅱ）的條件下，若
，求二面角
的大小.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖是某地區2012年至2018年生活垃圾無害化處理量（單位：萬噸）的折線圖.
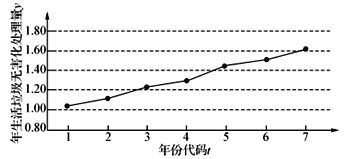
注：年份代碼
分別表示對應年份
.
（1）由折線圖看出，可用線性回歸模型擬合
與
的關系，請用相關系數
（
線性相關較強）加以說明；
（2）建立與的回歸方程(系數精確到0.01)，預測2019年該區生活垃圾無害化處理量.
（參考數據）
，
，
，
，
，
，
.
（參考公式）相關系數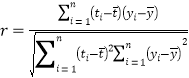
，在回歸方程
中斜率和截距的最小二乘估計公式分別為：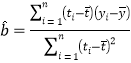
，
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】波羅尼斯（古希臘數學家，約公元前262-190年）的著作《圓錐曲線論》是古代世界光輝的科學成果，它將圓錐曲線的性質網羅殆盡幾乎使后人沒有插足的余地.他證明過這樣一個命題：平面內與兩定點距離的比為常數k（
且
）的點的軌跡是圓，后人將這個圓稱為阿波羅尼斯圓.現有
，
，則當的面積最大時，AC邊上的高為_______________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】用“算籌”表示數是我國古代計數方法之一，計數形式有縱式和橫式兩種，如圖1所示.金元時期的數學家李冶在《測圓海鏡》中記載：用“天元術”列方程，就是用算籌來表示方程中各項的系數.所謂“天元術”，即是一種用數學符號列方程的方法，“立天元一為某某”，意即“設
為某某”.如圖2所示的天元式表示方程
，其中
，
，…，
，
表示方程各項的系數，均為籌算數碼，在常數項旁邊記一“太”字或在一次項旁邊記一“元”字，“太”或“元”向上每層減少一次冪，向下每層增加一次冪.
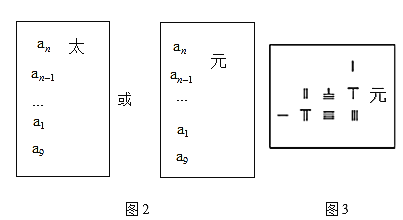
試根據上述數學史料，判斷圖3天元式表示的方程是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，以O為極點，x軸的正半軸為極軸，建立極坐標系，曲線C的極坐標方程為ρ2（cos2θ+3sin2θ）＝12，直線l的參數方程為
（t為參數），直線l與曲線C交于M，N兩點.
（1）若點P的極坐標為（2，π），求|PM||PN|的值；
（2）求曲線C的內接矩形周長的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，直線
與y軸交于點A，與拋物線
交于P，Q，點B與點A關于x軸對稱，連接QB，BP并延長分別與x軸交于點M，N.
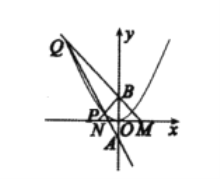
（1）若
，求拋物線C的方程；
（2）若
，求
外接圓的方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，在四棱錐
中，底面
為平行四邊形
∠ADC＝45°，
，
為
的中點，
⊥平面，
，
為
的中點．
(1)證明：
⊥平面
；
(2)求直線
與平面所成角的正切值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
