
【題目】新學年伊始,某中學學生社團開始招新,某高一新生對“海濟公益社”、“理科學社”、“高音低調樂社”很感興趣,假設她能被這三個社團接受的概率分別為 ![]() ,
, ![]() ,
, ![]() .
.
(1)求此新生被兩個社團接受的概率;
(2)設此新生最終參加的社團數為ξ,求ξ的分布列和數學期望.
【答案】
(1)解:設事件A表示“此新生能被海濟公益社接受”,事件B表示“此新生能理科學社接受”,
事件C表示“此新生能被高音低調樂社接受”,
則P(A)= ![]() ,P(B)=
,P(B)= ![]() ,P(C)=
,P(C)= ![]() ,
,
∴此新生被兩個社團接受的概率為:
P( ![]() +A
+A ![]() C+
C+ ![]() )=
)= ![]() +
+ ![]() +
+ ![]() =
= ![]() .
.
(2)解:由題意得ξ的可能取值為0,1,2,3,
P(ξ=0)= ![]() =
= ![]() ,
,
P(ξ=1)= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() +
+ ![]() +
+ ![]() =
= ![]() .
.
P(ξ=3)= ![]() =
= ![]() ,
,
∴ξ的分布列為:
X | 0 | 1 | 2 | 3 |
P | | | | |
E(X)= ![]() =
= ![]() .
.
【解析】(1)設事件A表示“此新生能被海濟公益社接受”,事件B表示“此新生能理科學社接受”,事件C表示“此新生能被高音低調樂社接受”,此新生被兩個社團接受的概率為:P( ![]() +A
+A ![]() C+
C+ ![]() ),由此能求出結果.(2)由題意得ξ的可能取值為0,1,2,3,分別求出相應的概率,由此能求出ξ的分布列和數學期望.
),由此能求出結果.(2)由題意得ξ的可能取值為0,1,2,3,分別求出相應的概率,由此能求出ξ的分布列和數學期望.
【考點精析】關于本題考查的離散型隨機變量及其分布列,需要了解在射擊、產品檢驗等例子中,對于隨機變量X可能取的值,我們可以按一定次序一一列出,這樣的隨機變量叫做離散型隨機變量.離散型隨機變量的分布列:一般的,設離散型隨機變量X可能取的值為x1,x2,.....,xi,......,xn,X取每一個值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,則稱表為離散型隨機變量X 的概率分布,簡稱分布列才能得出正確答案.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x+ ![]() ,g(x)=2x+a,若x1∈[
,g(x)=2x+a,若x1∈[ ![]() ,3],x2∈[2,3],使得f(x1)≥g(x2),則實數a的取值范圍是( )
,3],x2∈[2,3],使得f(x1)≥g(x2),則實數a的取值范圍是( )
A.a≤1
B.a≥1
C.a≤0
D.a≥0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直線過點P![]() 且與x軸、y軸的正半軸分別交于A,B兩點,O為坐標原點,是否存在這樣的直線滿足下列條件:①△AOB的周長為12;②△AOB的面積為6.若存在,求出方程;若不存在,請說明理由.
且與x軸、y軸的正半軸分別交于A,B兩點,O為坐標原點,是否存在這樣的直線滿足下列條件:①△AOB的周長為12;②△AOB的面積為6.若存在,求出方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】公元263年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形的面積可無限接近圓的面積,并創立了“割圓術”,利用“割圓術”,劉徽得到了圓周率精確到小數點后兩位的近似值3.14,這就是著名的“徽率”,如圓是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出的值為( )(參考數據:sin15°=0.2588,sin7.50=0.1305) 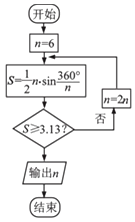
A.12
B.24
C.48
D.96
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)判斷函數![]() 的奇偶性,并給出證明;
的奇偶性,并給出證明;
(2)解不等式: ![]() ;
;
(3)若函數![]() 在
在![]() 上單調遞減,比較f(2)+f(4)+…+f(2n)與2n(n∈N*)的大小關系,并說明理由.
上單調遞減,比較f(2)+f(4)+…+f(2n)與2n(n∈N*)的大小關系,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax﹣lnx;g(x)= ![]() .
.
(1)討論函數f(x)的單調性;
(2)求證:若a=e(e是自然常數),當x∈[1,e]時,f(x)≥e﹣g(x)恒成立;
(3)若h(x)=x2[1+g(x)],當a>1時,對于x1∈[1,e],x0∈[1,e],使f(x1)=h(x0),求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大衍數列,來源于中國古代著作《乾坤譜》中對易傳“大衍之數五十”的推論.其前10項為:0、2、4、8、12、18、24、32、40、50.通項公式: 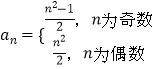 ,如果把這個數列{an}排成如圖形狀,并記A(m,n)表示第m行中從左向右第n個數,則A(10,4)的值為( )
,如果把這個數列{an}排成如圖形狀,并記A(m,n)表示第m行中從左向右第n個數,則A(10,4)的值為( ) 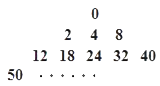
A.1200
B.1280
C.3528
D.3612
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點O為坐標原點,橢圓E: ![]() (a≥b>0)的右頂點為A,上頂點為B,過點O且斜率為
(a≥b>0)的右頂點為A,上頂點為B,過點O且斜率為 ![]() 的直線與直線AB相交M,且
的直線與直線AB相交M,且 ![]() .
.
(Ⅰ)求橢圓E的離心率e;
(Ⅱ)PQ是圓C:(x﹣2)2+(y﹣1)2=5的一條直徑,若橢圓E經過P,Q兩點,求橢圓E的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com