【題目】(導學號：05856263)
已知拋物線y2＝2px(p>0)的準線與x軸交于點N，過點N作圓M：(x－2)2＋y2＝1的兩條切線，切點為P、Q，且|PQ|＝
.
(Ⅰ)求拋物線的方程；
(Ⅱ)過拋物線的焦點F作斜率為k1的直線與拋物線交于A、B兩點，A、B兩點的橫坐標均不為2，連接AM，BM并延長分別交拋物線于C、D兩點，設直線CD的斜率為k2，問
是否為定值？若是，求出該定值；若不是，說明理由．
【答案】(1) y2＝4x ，(2) 定值2
【解析】試題分析：（1）求得拋物線的準線方程，可得N的坐標，圓M的圓心和半徑，可得四點N，P，M，Q共圓，且MN為直徑，設為2R，在△PMQ中，運用余弦定理和正弦定理，可得2R=3，求得p=2，即可得到拋物線的方程；
（2）求得拋物線y2=4x的焦點為F（1，0），設A（x1，y1），B（x2，y2），C（x3，y3），D（x4，y4），運用直線的斜率公式，求得k1，k2，及
，設出直線AC，BD和AB的方程，聯立拋物線的方程，運用韋達定理，計算即可得到定值2．
試題解析：
(Ⅰ)由已知得N(－
，0)，M(2,0)．設PQ與x軸交于點R，由圓的對稱性可知，|PR|＝
.
于是|MR|＝
＝
.
由△PNM∽△RPM得
＝
，
∴|NM|＝3，即2＋＝3，p＝2.
故拋物線的方程為y2＝4x.
(Ⅱ)設A(x1，y1)，B(x2，y2)，C(x3，y3)，D(x4，y4)，
則k1＝
＝
＝
，
同理k2＝
.
設AC所在直線的方程為x＝ty＋2，
與y2＝4x聯立，得y2－4ty－8＝0，所以y1y3＝－8，同理y2y4＝－8，
所以k2＝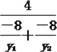
＝(－
)·
.
設AB所在直線的方程x＝my＋1與y2＝4x聯立，
得y2－4my－4＝0，所以y1y2＝－4，
所以k2＝(－)·＝
，所以
＝2，即為定值2.
科目：高中數學 來源： 題型：
【題目】某P2P平臺需要了解該平臺投資者的大致年齡分布，發現其投資者年齡大多集中在區間[20,50]歲之間，對區間[20,50]歲的人群隨機抽取20人進行了一次理財習慣調查，得到如下統計表和各年齡段人數頻率分布直方圖：
組數 | 分組 | 人數(單位：人) |
第一組 | [20,25) | 2 |
第二組 | [25,30) | a |
第三組 | [30,35) | 5 |
第四組 | [35,40) | 4 |
第五組 | [40,45) | 3 |
第六組 | [45,50] | 2 |
(Ⅰ)求a的值并畫出頻率分布直方圖；
(Ⅱ)在統計表的第五與第六組的5人中，隨機選取2人，求這2人的年齡都小于45歲的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直三棱柱ABC－A1B1C1中，AB＝1，AC＝2，BC＝
，D，E分別是AC1，BB1的中點，則直線DE與平面BB1C1C所成角的正弦值為________．
查看答案和解析>>
科目：高中數學 來源： 題型：
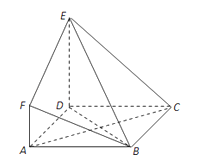
【題目】如圖，ABCD是邊長為3的正方形，DE⊥平面ABCD，AF∥DE，DE=3AF，BE與平面ABCD所成角為60°．
（Ⅰ）求證：AC⊥平面BDE；
（Ⅱ）求二面角F﹣BE﹣D的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(導學號：05856308)(12分)
如圖，∠ABC＝
，O為AB上一點，3OB＝3OC＝2AB，PO⊥平面ABC,2DA＝2AO＝PO，OA＝1，且DA∥PO.
(Ⅰ)求證：平面PBD⊥平面COD；
(Ⅱ)求點O到平面BDC的距離．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
