
【題目】已知關于x的一元二次不等式ax2+2x+b>0的解集為{x|x≠c},則![]() (其中a+c≠0)的取值范圍為_____.
(其中a+c≠0)的取值范圍為_____.
【答案】(﹣∞,﹣6]∪[6,+∞)
【解析】
由條件利用二次函數的性質可得ac=﹣1,ab=1, 即c=-b將![]() 轉為(a﹣b)+
轉為(a﹣b)+![]() ,利用基本不等式求得它的范圍.
,利用基本不等式求得它的范圍.
因為一元二次不等式ax2+2x+b>0的解集為{x|x≠c},由二次函數圖像的性質可得a>0,二次函數的對稱軸為x=![]() =c,△=4﹣4ab=0,
=c,△=4﹣4ab=0,
∴ac=﹣1,ab=1,∴c=![]() ,b=
,b=![]() ,即c=-b,
,即c=-b,
則![]() =
=![]() =(a﹣b)+
=(a﹣b)+![]() ,
,
當a﹣b>0時,由基本不等式求得(a﹣b)+![]() ≥6,
≥6,
當a﹣b<0時,由基本不等式求得﹣(a﹣b)﹣![]() ≥6,即(a﹣b)+
≥6,即(a﹣b)+![]() ≤﹣6,
≤﹣6,
故![]() (其中a+c≠0)的取值范圍為:(﹣∞,﹣6]∪[6,+∞),
(其中a+c≠0)的取值范圍為:(﹣∞,﹣6]∪[6,+∞),
故答案為:(﹣∞,﹣6]∪[6,+∞).


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案科目:高中數學 來源: 題型:
【題目】某校舉行漢字聽寫比賽,為了了解本次比賽成績情況,從得分不低于50分的試卷中隨機抽取100名學生的成績(得分均為整數,滿分100分)進行統計,請根據頻率分布表中所提供的數據,解答下列問題:

(1)求![]() 的值;
的值;
(2)若從成績較好的第3、4、5組中按分層抽樣的方法抽取6人參加市漢字聽寫比賽,并從中選出2人做種子選手,求2人中至少有1人是第4組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動點P與兩個定點O(0,0),A(3,0)的距離的比值為2,點P的軌跡為曲線C.
(1)求曲線C的軌跡方程
(2)過點(﹣1,0)作直線與曲線C交于A,B兩點,設點M坐標為(4,0),求△ABM面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C:y2=2px(p>0)的焦點為F,過F且斜率為![]() 的直線l與拋物線C交于A,B兩點,B在x軸的上方,且點B的橫坐標為4.
的直線l與拋物線C交于A,B兩點,B在x軸的上方,且點B的橫坐標為4.
(1)求拋物線C的標準方程;
(2)設點P為拋物線C上異于A,B的點,直線PA與PB分別交拋物線C的準線于E,G兩點,x軸與準線的交點為H,求證:HGHE為定值,并求出定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某沿海城市的海邊有兩條相互垂直的直線型公路l1、l2,海岸邊界MPN近似地看成一條曲線段.為開發旅游資源,需修建一條連接兩條公路的直線型觀光大道AB,且直線AB與曲線MPN有且僅有一個公共點P(即直線與曲線相切),如圖所示.若曲線段MPN是函數![]() 圖象的一段,點M到l1、l2的距離分別為8千米和1千米,點N到l2的距離為10千米,以l1、l2分別為x、y軸建立如圖所示的平面直角坐標系xOy,設點P的橫坐標為p.
圖象的一段,點M到l1、l2的距離分別為8千米和1千米,點N到l2的距離為10千米,以l1、l2分別為x、y軸建立如圖所示的平面直角坐標系xOy,設點P的橫坐標為p.
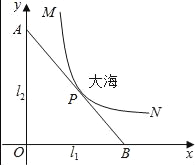
(1)求曲線段MPN的函數關系式,并指出其定義域;
(2)若某人從點O沿公路至點P觀景,要使得沿折線OAP比沿折線OBP的路程更近,求p的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中
(1)在等差數列![]() 中,
中,![]() 是
是![]() 的充要條件;
的充要條件;
(2)已知等比數列![]() 為遞增數列,且公比為
為遞增數列,且公比為![]() ,若
,若![]() ,則當且僅當
,則當且僅當![]() ;
;
(3)若數列![]() 為遞增數列,則
為遞增數列,則![]() 的取值范圍是
的取值范圍是![]() ;
;
(4)已知數列![]() 滿足
滿足![]() ,則數列
,則數列![]() 的通項公式為
的通項公式為![]()
(5)若![]() 是等比數列
是等比數列![]() 的前
的前![]() 項的和,且
項的和,且![]() ;(其中
;(其中![]() 、
、![]() 是非零常數,
是非零常數,![]() ),則A+B為零.
),則A+B為零.
其中正確命題是_________(只需寫出序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正四面體ABCD中,點E,F分別是AB,BC的中點,則下列命題正確的序號是______
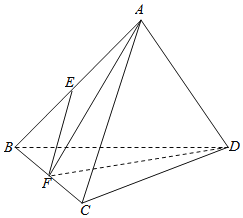
①異面直線AB與CD所成角為90°;
②直線AB與平面BCD所成角為60°;
③直線EF∥平面ACD
④平面AFD⊥平面BCD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在四棱錐![]() 中,四邊形
中,四邊形![]() 為矩形,
為矩形, ![]() 為等腰三角形,
為等腰三角形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() 的中點.
的中點.

(1)證明: ![]() 平面
平面![]() ;
;
(2)證明:平面![]() 平面
平面![]() ;
;
(3)求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com