
【題目】已知函數![]() .
.
(1)判斷函數![]() 的零點的個數并說明理由;
的零點的個數并說明理由;
(2)求函數![]() 零點所在的一個區間,使這個區間的長度不超過
零點所在的一個區間,使這個區間的長度不超過![]() ;
;
(3)若![]() ,對于任意的
,對于任意的![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)一個,理由見解析;(2)![]() ;
;![]() .
.
【解析】
(1)分析函數![]() 的單調性,結合零點存在定理可得出結論;
的單調性,結合零點存在定理可得出結論;
(2)先可求得函數![]() 的零點所在的一個區間為
的零點所在的一個區間為![]() ,然后利用二分法可得出
,然后利用二分法可得出![]() 的一個零點所在的區間,且這個區間的長度不超過
的一個零點所在的區間,且這個區間的長度不超過![]() ;
;
(3)由題意可知,![]() ,利用函數
,利用函數![]() 的單調性求出該函數在區間
的單調性求出該函數在區間![]() 的最大值
的最大值![]() ,將問題轉化為關于
,將問題轉化為關于![]() 的不等式
的不等式![]() 對任意的
對任意的![]() 恒成立,可得出
恒成立,可得出![]() ,由此可解出實數
,由此可解出實數![]() 的取值范圍.
的取值范圍.
(1)由題易知:函數![]() 的定義域為
的定義域為![]() ,且在
,且在![]() 上連續,
上連續,
![]() ,
,![]() ,
,![]() ,
,
![]() 函數
函數![]() 和
和![]() 在
在![]() 上都是增函數,
上都是增函數,
所以,函數![]() 在
在![]() 上是增函數,
上是增函數,
因此,函數![]() 在
在![]() 上有且只有一個零點;
上有且只有一個零點;
(2)設函數![]() 的零點為
的零點為![]() ,由(1)知:
,由(1)知:![]() ,
,![]() ,
,![]() ,
,
取![]() ,
,![]() ,
,
![]() ,
,![]() 且
且![]() ,
, ![]() 即為符合條件的區間;
即為符合條件的區間;
(3)當![]() 時,對于任意的
時,對于任意的![]() ,不等式
,不等式![]() 恒成立等價于
恒成立等價于
![]() ,
,![]() ,
,![]() .
.
由函數![]() 在
在![]() 上是增函數,可知
上是增函數,可知![]() ,
,
![]() 對任意
對任意![]() 恒成立,
恒成立,![]() 對任意
對任意![]() 恒成立,
恒成立,
![]() ,解得
,解得![]() ,
,
因此,![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
【題目】風景秀美的寶湖畔有四棵高大的銀杏樹,記作A,B,P,Q,湖岸部分地方圍有鐵絲網不能靠近.欲測量P,Q兩棵樹和A,P兩棵樹之間的距離,現可測得A,B兩點間的距離為100 m,∠PAB=75°,∠QAB=45°,∠PBA=60°,∠QBA=90°,如圖所示.則P,Q兩棵樹和A,P兩棵樹之間的距離各為多少?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海水養殖場進行某水產品的新、舊網箱養殖方法的產量對比,收獲時各隨機抽取了100個網箱,測量各箱水產品的產量(單位:kg), 其頻率分布直方圖如下:

(1)記A表示事件“舊養殖法的箱產量低于50 kg”,估計A的概率;
(2)填寫下面列聯表,并根據列聯表判斷是否有99%的把握認為箱產量與養殖方法有關:
箱產量<50 kg | 箱產量≥50 kg | |
舊養殖法 | ||
新養殖法 |
(3)根據箱產量的頻率分布直方圖,對這兩種養殖方法的優劣進行比較.
附:
P( | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,四棱錐P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=![]() AD,E,F分別為線段AD,PC的中點.
AD,E,F分別為線段AD,PC的中點.
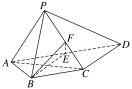
(1)求證:AP∥平面BEF;
(2)求證:BE⊥平面PAC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四面體ABCD中,![]() 與
與![]() 都是邊長為8的正三角形,點O是線段BC的中點.
都是邊長為8的正三角形,點O是線段BC的中點.
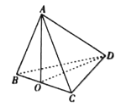
(1)證明:![]() .
.
(2)若![]() 為銳角,且四面體ABCD的體積為
為銳角,且四面體ABCD的體積為![]() 求側面ACD的面積.
求側面ACD的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某生產基地有五臺機器,現有五項工作待完成,每臺機器完成每項工作后獲得的效益值如表所示.若每臺機器只完成一項工作,且完成五項工作后獲得的效益值總和最大,則下列敘述錯誤的的是_____________.
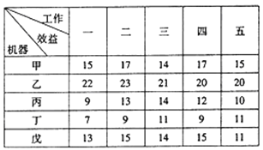
①甲只能承擔第四項工作
②乙不能承擔第二項工作
③丙可以不承擔第三項工作
④丁可以承擔第三項工作
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設關于某設備的使用年限x和所支出的維修費用y(萬元)有如下的統計資料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
維修費用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由資料知y對x呈線性相關關系.
(1)請畫出上表數據的散點圖;
(2)請根據最小二乘法求出線性回歸方程![]() 的回歸系數a,b;
的回歸系數a,b;
(3)估計使用年限為10年時,維修費用是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com