
【題目】已知函數![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)若![]() 對
對![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】點![]() 分別是正方體
分別是正方體![]() 的棱
的棱![]() 的中點,如圖所示,則下列命題中的真命題是________(寫出所有真命題的編號).
的中點,如圖所示,則下列命題中的真命題是________(寫出所有真命題的編號).
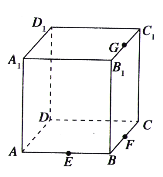
①以正方體的頂點為頂點的三棱錐的四個面中最多只有三個面是直角三角形;②點![]() 在直線
在直線![]() 上運動時,總有
上運動時,總有![]() ;③點
;③點![]() 在直線
在直線![]() 上運動時,三棱錐
上運動時,三棱錐![]() 的體積的定值;④若點
的體積的定值;④若點![]() 是正方體的面
是正方體的面![]() 內的一動點,且
內的一動點,且![]() 到點
到點![]() 和
和![]() 距離相等,則點
距離相等,則點![]() 的軌跡是一條線段.
的軌跡是一條線段.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若函數y=f(x)為偶函數,求k 的值;
(2)求函數y=f(x)在區間[0,4]上的最大值;
(3)若方程f(x)=0 有且僅有一個根,求實數k 的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三課外興趣小組為了解高三同學高考結束后是否打算觀看2018年足球世界杯比賽的情況,從全校高三年級1500名男生、1000名女生中按分層抽樣的方式抽取125名學生進行問卷調查,情況如下表:
打算觀看 | 不打算觀看 | |
女生 | 20 | b |
男生 | c | 25 |
(1)求出表中數據b,c;
(2)判斷是否有99%的把握認為觀看2018年足球世界杯比賽與性別有關;
(3)為了計算“從10人中選出9人參加比賽”的情況有多少種,我們可以發現它與“從10人中選出1人不參加比賽”的情況有多少種是一致的.現有問題:在打算觀看2018年足球世界杯比賽的同學中有5名男生、2名女生來自高三(5)班,從中推選5人接受校園電視臺采訪,請根據上述方法,求被推選出的5人中恰有四名男生、一名女生的概率.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附: 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一只紅鈴蟲的產卵數y和溫度x有關,現收集了6組觀測數據于下表中,通過散點圖可以看出樣本點分布在一條指數型函數y=![]() 的圖象的周圍.
的圖象的周圍.
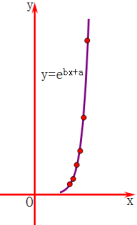
(1)試求出y關于x的上述指數型的回歸曲線方程(結果保留兩位小數);
(2)試用(1)中的回歸曲線方程求相應于點(24,17)的殘差![]() .(結果保留兩位小數)
.(結果保留兩位小數)
溫度x(°C) | 20 | 22 | 24 | 26 | 28 | 30 |
產卵數y(個) | 6 | 9 | 17 | 25 | 44 | 88 |
z=lny | 1.79 | 2.20 | 2.83 | 3.22 | 3.78 | 4.48 |
幾點說明:
①結果中的![]() 都應按題目要求保留兩位小數.但在求
都應按題目要求保留兩位小數.但在求![]() 時請將
時請將![]() 的值多保留一位即用保留三位小數的結果代入.
的值多保留一位即用保留三位小數的結果代入.
②計算過程中可能會用到下面的公式:回歸直線方程的斜率![]() =
= =
= ,截距
,截距![]() .
.
③下面的參考數據可以直接引用:![]() =25,
=25,![]() =31.5,
=31.5,![]() ≈3.05,
≈3.05,![]() =5248,
=5248,![]() ≈476.08,
≈476.08,![]() ,ln18.17≈2.90.
,ln18.17≈2.90.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為凈化新安江水域的水質,市環保局于2017年底在新安江水域投入一些蒲草,這些蒲草在水中的蔓延速度越來越快,2018年二月底測得蒲草覆蓋面積為![]() ,2018年三月底測得覆蓋面積為
,2018年三月底測得覆蓋面積為![]() ,蒲草覆蓋面積
,蒲草覆蓋面積![]() (單位:
(單位:![]() )與月份
)與月份![]() (單位:月)的關系有兩個函數模型
(單位:月)的關系有兩個函數模型![]() 與
與![]() 可供選擇.
可供選擇.
(Ⅰ)分別求出兩個函數模型的解析式;
(Ⅱ)若市環保局在2017年年底投放了![]() 的蒲草,試判斷哪個函數模型更合適?并說明理由;
的蒲草,試判斷哪個函數模型更合適?并說明理由;
(Ⅲ)利用(Ⅱ)的結論,求蒲草覆蓋面積達到![]() 的最小月份.
的最小月份.
(參考數據:![]() ,
,![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com