
【題目】如圖,多面體![]() 中,面
中,面![]() 為矩形,面
為矩形,面![]() 面
面![]() ,
,![]() .
.
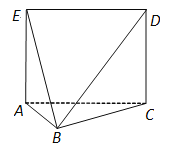
(1)求證:面![]() 面
面![]() ;
;
(2)已知多面體![]() 各頂點(diǎn)均在同一球面上,且該球的表面積為
各頂點(diǎn)均在同一球面上,且該球的表面積為![]() ,
,![]() ,當(dāng)這個(gè)多面體的體積取得最大值時(shí)求其側(cè)視圖的面積.
,當(dāng)這個(gè)多面體的體積取得最大值時(shí)求其側(cè)視圖的面積.
【答案】(1)見解析; (2)![]() .
.
【解析】
(1)由已知面面垂直得線面垂直,從而得線線垂直,再結(jié)合已知線線垂直得線面垂直,證得面面垂直;
(2)找出球心為![]() 與
與![]() 的交點(diǎn)
的交點(diǎn)![]() ,由球面積求出直徑
,由球面積求出直徑![]() 的長,得
的長,得![]() ,可得多面體的體積取得最大值時(shí),
,可得多面體的體積取得最大值時(shí),![]() 到
到![]() 的距離取最大值
的距離取最大值![]() ,從而易得側(cè)視圖面積.
,從而易得側(cè)視圖面積.
(1)面![]() 為矩形,面
為矩形,面![]() 面
面![]() ,
,![]() ,面
,面![]() 面
面![]()
![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() ,又
,又![]() ,
,![]()
∴![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,
,
∴面![]() 面
面![]() .
.
(2)設(shè)![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() ,
,![]() 是
是![]() 中點(diǎn),連接
中點(diǎn),連接![]() ,則
,則![]() ,從而
,從而![]() 平面
平面![]() 主,
主,![]() 是
是![]() 外心,∴
外心,∴![]() 是多面體
是多面體![]() 中外接球球心,
中外接球球心,
由![]() ,得
,得![]() ,又
,又![]() ,
,
∴![]() .又
.又![]() ,
,![]() 為直角三角形,
為直角三角形,
∴當(dāng)![]() 斜邊
斜邊![]() 上的高等于
上的高等于![]() 時(shí),體積取得最大值.
時(shí),體積取得最大值.
此時(shí)其側(cè)視圖也為直角三角形,面積為![]() .
.



 名校課堂系列答案
名校課堂系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“中國剩余定理”又稱“孫子定理”,最早可見于中國南北朝時(shí)期的數(shù)學(xué)著作《孫子算經(jīng)》卷下第二十六題,叫做“物不知數(shù)”,原文如下:今有物不知其數(shù),三三數(shù)之剩二,五五數(shù)之剩三,七七數(shù)之剩二.問物幾何?現(xiàn)有這樣一個(gè)相關(guān)的問題:將1到2020這2020個(gè)自然數(shù)中被5除余3且被7除余2的數(shù)按照從小到大的順序排成一列,構(gòu)成一個(gè)數(shù)列,則該數(shù)列各項(xiàng)之和為( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 為奇函數(shù),且
為奇函數(shù),且![]() 的極小值為
的極小值為![]() .
.![]() 為函數(shù)
為函數(shù)![]() 的導(dǎo)函數(shù).
的導(dǎo)函數(shù).
(1)求![]() 和
和![]() 的值;
的值;
(2)若關(guān)于![]() 的方程
的方程![]() 有三個(gè)不等的實(shí)數(shù)根,求實(shí)數(shù)
有三個(gè)不等的實(shí)數(shù)根,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
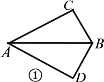
【題目】在平面四邊形![]() (圖①)中,
(圖①)中,![]() 與
與![]() 均為直角三角形且有公共斜邊
均為直角三角形且有公共斜邊![]() ,設(shè)
,設(shè)![]() ,∠
,∠![]() ,∠
,∠![]() ,將
,將![]() 沿
沿![]() 折起,構(gòu)成如圖②所示的三棱錐
折起,構(gòu)成如圖②所示的三棱錐![]() ,且使
,且使![]() =
=![]() .
.
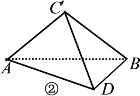
(1)求證:平面![]() ⊥平面
⊥平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】橢圓![]()
![]() 的離心率為
的離心率為![]() ,其右焦點(diǎn)到點(diǎn)
,其右焦點(diǎn)到點(diǎn)![]() 的距離為
的距離為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點(diǎn)(
兩點(diǎn)(![]() ,
,![]() 不是左右頂點(diǎn)),且以
不是左右頂點(diǎn)),且以![]() 為直徑的圓過橢圓
為直徑的圓過橢圓![]() 的右頂點(diǎn),求證直線
的右頂點(diǎn),求證直線![]() 過定點(diǎn),并求出該定點(diǎn)的坐標(biāo).
過定點(diǎn),并求出該定點(diǎn)的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() (
(![]() ,
,![]() 是自然對數(shù)的底數(shù)).
是自然對數(shù)的底數(shù)).
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)曲線![]() 在
在![]() 、
、![]() 處的切線平行,線段
處的切線平行,線段![]() 的中點(diǎn)為
的中點(diǎn)為![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系xOy中,曲線C的參數(shù)方程為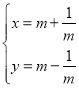 (m為參數(shù)),以坐標(biāo)原點(diǎn)O為極點(diǎn),x軸的正半軸為極軸建立極坐標(biāo)系,直線
(m為參數(shù)),以坐標(biāo)原點(diǎn)O為極點(diǎn),x軸的正半軸為極軸建立極坐標(biāo)系,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]()
(1)求曲線C和直線![]() 的直角坐標(biāo)系方程;
的直角坐標(biāo)系方程;
(2)已知![]() 直線
直線![]() 與曲線C相交于A,B兩點(diǎn),求
與曲線C相交于A,B兩點(diǎn),求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】將函數(shù)![]() 向左平移
向左平移![]() 個(gè)單位,得到
個(gè)單位,得到![]() 的圖象,則
的圖象,則![]() 滿足( )
滿足( )
A.圖象關(guān)于點(diǎn)![]() 對稱,在區(qū)間
對稱,在區(qū)間![]() 上為增函數(shù)
上為增函數(shù)
B.函數(shù)最大值為2,圖象關(guān)于點(diǎn)![]() 對稱
對稱
C.圖象關(guān)于直線![]() 對稱,在
對稱,在![]() 上的最小值為1
上的最小值為1
D.最小正周期為![]() ,
,![]() 在
在![]() 有兩個(gè)根
有兩個(gè)根
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】![]() 年
年![]() 月,第二屆“一帶一路”國際合作高峰論壇在北京成功舉辦.“一帶一路”是由中國倡議,積極發(fā)展中國與沿線國家經(jīng)濟(jì)合作伙伴關(guān)系的區(qū)域合作平臺,共同打造政治互信、經(jīng)濟(jì)融合、文化包容的利益、命運(yùn)和責(zé)任共同體.深受有關(guān)國家的積極響應(yīng).某公司搭乘這班快車,計(jì)劃對沿線甲、乙、丙三個(gè)國進(jìn)行投資,其中選擇一國投資兩次,其余兩國各投資一次.共四次投資.每次投資,公司設(shè)置投資金額共有
月,第二屆“一帶一路”國際合作高峰論壇在北京成功舉辦.“一帶一路”是由中國倡議,積極發(fā)展中國與沿線國家經(jīng)濟(jì)合作伙伴關(guān)系的區(qū)域合作平臺,共同打造政治互信、經(jīng)濟(jì)融合、文化包容的利益、命運(yùn)和責(zé)任共同體.深受有關(guān)國家的積極響應(yīng).某公司搭乘這班快車,計(jì)劃對沿線甲、乙、丙三個(gè)國進(jìn)行投資,其中選擇一國投資兩次,其余兩國各投資一次.共四次投資.每次投資,公司設(shè)置投資金額共有![]() 、
、![]() 、
、![]() 、
、![]() (億元)四個(gè)檔次,其中
(億元)四個(gè)檔次,其中![]() 檔投資至多為一次,
檔投資至多為一次,![]() 檔投資至少為一次,
檔投資至少為一次,![]() 檔投資不能在同一國中被投兩次,則不同的投資方案(不考慮投資的先后順序)有( )
檔投資不能在同一國中被投兩次,則不同的投資方案(不考慮投資的先后順序)有( )
A.![]() 種B.
種B.![]() 種C.
種C.![]() 種D.以上答案均不正確
種D.以上答案均不正確
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com