
【題目】已知公比不為1的等比數列{an}的前5項積為243,且2a3為3a2和a4的等差中項.
(1)求數列{an}的通項公式an;
(2)若數列{bn}滿足bn=bn﹣1log3an+2(n≥2且n∈N*),且b1=1,求數列 ![]() 的前n項和Sn .
的前n項和Sn .
【答案】
(1)解:由前5項積為243,即為a1a2a3a4a5=243,
即有a1a5=a2a4=a32,即a35=243,
得:a3=3,設等比數列的公比為q,
由2a3為3a2和a4的等差中項得:4a3=3a2+a4,
即 ![]() ,
,
由公比不為1,解得:q=3,
所以an=a3qn﹣3,
即 ![]()
(2)解:由bn=bn﹣1log3an+2=bn﹣1n,
得 ![]() ,
,
數列 ![]() ,
,
所以它的前n項和 ![]()
【解析】(1)運用等比數列的性質可得a3=3,設等比數列的公比為q,運用等差數列中項的性質,結合等比數列通項公式,解得q=3,即可得到所求數列{an}的通項公式;(2)求得bn=bn﹣1log3an+2=bn﹣1n,運用數列恒等式bn=b1 ![]() …
… ![]() =n!,求出
=n!,求出 ![]() ,運用裂項相消求和即可得到所求和.
,運用裂項相消求和即可得到所求和.


 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:
【題目】已知在平面直角坐標系xOy中,以O為極點,x軸的正半軸為極軸,建立極坐標系.曲線C1的極坐標方程為ρ=4cosθ,直線l: 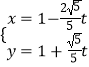 (
( ![]() 為參數).
為參數).
(1)求曲線C1的直角坐標方程及直線l的普通方程;
(2)若曲線C2的參數方程為 ![]() (α為參數),曲線P(x0 , y0)上點P的極坐標為
(α為參數),曲線P(x0 , y0)上點P的極坐標為 ![]() ,Q為曲線C2上的動點,求PQ的中點M到直線l距離的最大值.
,Q為曲線C2上的動點,求PQ的中點M到直線l距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點F(1,0),點A是直線l1:x=﹣1上的動點,過A作直線l2 , l1⊥l2 , 線段AF的垂直平分線與l2交于點P.
(Ⅰ)求點P的軌跡C的方程;
(Ⅱ)若點M,N是直線l1上兩個不同的點,且△PMN的內切圓方程為x2+y2=1,直線PF的斜率為k,求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是定義域為(0,+∞)的單調函數,若對任意的x∈(0,+∞),都有 ![]() ,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在區間(0,3]上有兩解,則實數a的取值范圍是( )
,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在區間(0,3]上有兩解,則實數a的取值范圍是( )
A.0<a≤5
B.a<5
C.0<a<5
D.a≥5
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱柱ABC﹣A1B1C1中,已知側面ABB1A1是菱形,側面BCC1B1是正方形,點A1在底面ABC的投影為AB的中點D. 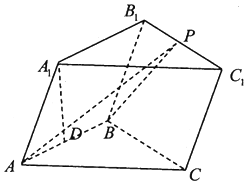
(1)證明:平面AA1B1B⊥平面BB1C1C;
(2)設P為B1C1上一點,且 ![]() ,求二面角A1﹣AB﹣P的正弦值.
,求二面角A1﹣AB﹣P的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,以坐標原點為極點,
中,以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系.已知點
軸的正半軸為極軸建立極坐標系.已知點![]() 的直角坐標為
的直角坐標為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 過點
過點![]() 且與曲線
且與曲線![]() 相交于
相交于![]() ,
,![]() 兩點.
兩點.
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() ,求直線
,求直線![]() 的直角坐標方程.
的直角坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠新研發了一種產品,該產品每件成本為5元,將該產品按事先擬定的價格進行銷售,得到如下數據:
單價 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
銷量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求銷量![]() (件)關于單價
(件)關于單價![]() (元)的線性回歸方程
(元)的線性回歸方程![]() ;
;
(2)若單價定為10元,估計銷量為多少件;
(3)根據銷量![]() 關于單價
關于單價![]() 的線性回歸方程,要使利潤
的線性回歸方程,要使利潤![]() 最大,應將價格定為多少?
最大,應將價格定為多少?
參考公式: ,
,![]() .參考數據:
.參考數據:![]() ,
,![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com