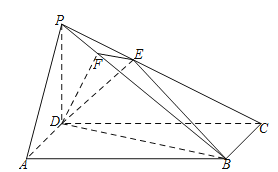
【題目】如圖，在四棱錐
中，底面
是長方形，側棱
底面，且
，過D作
于F，過F作
交 PC于E.
（Ⅰ）證明：
平面PBC；
（Ⅱ）求平面
與平面所成二面角的余弦值.
【答案】（Ⅰ）見解析; （Ⅱ）
.
【解析】【試題分析】（Ⅰ）依據題設運用直線與平面垂直的判定定理推證; （Ⅱ）依據題設條件運用二面角的平面角的定義求解或運用向量的數量積公式求解：.
解法一：（Ⅰ）因為
底面
，所以
，
由底面
為長方形，有
，而
，
所以
. 而
，所以
. ………………………2分
又因為
， 
所以
平面
. 而
，所以
. ………………………4分
又
，
，所以
平面
. ………………………6分
（Ⅱ）如圖1，在面內，延長
與
交于點
，則
是平面與平面
的交線. 由（Ⅰ）知，
，所以
. ………………………8分
又因為
底面，所以
. 而
，所以
.
故
是面與面所成二面角的平面角， ………………………10分
在Rt△PDB中, 由 
,
故面
與面所成二面角的余弦為
. ………………………12分
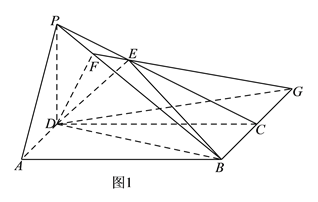
解法二：如圖2, 由
，所以
是平面的一個法向量； ……………………………………8分
由（Ⅰ）知，
，所以
是平面的一個法向量 ……………………………………10分
設平面與平面所成二面角為
則
，
故面與面所成二面角的余弦為. ……………………………………12分
口算題卡加應用題集訓系列答案科目：高中數學 來源： 題型：
【題目】對于定義在
上的函數
，若存在距離為
的兩條直線
和
，使得對任意
都有
恒成立，則稱函數
有一個寬度為
的通道，給出下列函數：①
；②
；③
；④
.其中在區間
上通道寬度可以為1的函數的個數是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四邊形ABCD為菱形，G為AC與BD的交點，BE⊥平面ABCD，
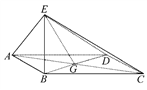
(1)證明：平面AEC⊥平面BED.
(2)若∠ABC=120°，AE⊥EC，三棱錐E-ACD的體積為
，求該三棱錐的側面積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，函數
.
（1）若
的定義域為
，求實數
的取值范圍；
（2）當
時，求函數
的最小值
；
（3）是否存在非負實數
，使得函數
的定義域為
，值域為
，若存在，求出
的值；若不存在，則說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
．
（Ⅰ）若f（1）=0，求函數f（x）的最大值；
（Ⅱ）令
，討論函數g（x）的單調區間；
（Ⅲ）若a=2，正實數x1，x2滿足
證明
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
