
【題目】“微信運動”已成為當下熱門的健身方式,小王的微信朋友圈內也有大量好友參與了“微信運動”,他隨機選取了其中的![]() 人(男、女各
人(男、女各![]() 人),記錄了他們某一天的走路步數,并將數據整理如下:
人),記錄了他們某一天的走路步數,并將數據整理如下:
步量 性別 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
(1)已知某人一天的走路步數超過![]() 步被系統評定“積極型”,否則為“懈怠型”,根據題意完成下面的
步被系統評定“積極型”,否則為“懈怠型”,根據題意完成下面的![]() 列聯表,并據此判斷能否有
列聯表,并據此判斷能否有![]() 以上的把握認為“評定類型”與“性別”有關?
以上的把握認為“評定類型”與“性別”有關?
積極型 | 懈怠型 | 總計 | |
男 | |||
女 | |||
總計 |
附:![]() ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
(2)若小王以這![]() 位好友該日走路步數的頻率分布來估計其所有微信好友每日走路步數的概率分布,現從小王的所有微信好友中任選
位好友該日走路步數的頻率分布來估計其所有微信好友每日走路步數的概率分布,現從小王的所有微信好友中任選![]() 人,其中每日走路不超過
人,其中每日走路不超過![]() 步的有
步的有![]() 人,超過
人,超過![]() 步的有
步的有![]() 人,設
人,設![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
【答案】(1)答案見解析;(2)答案見解析.
【解析】試題分析:
(1)有條件中給出的數據可得列聯表,求得![]() 后根據臨界值表中的數據可得判斷.(2)由題意得從小王的微信好友中任選一人,其每日走路步數不超過
后根據臨界值表中的數據可得判斷.(2)由題意得從小王的微信好友中任選一人,其每日走路步數不超過![]() 步的概率為
步的概率為![]() ,超過
,超過![]() 步的概率為
步的概率為![]() .然后判斷得到隨機變量
.然后判斷得到隨機變量![]() 的所有可能取值,分別求出概率后得到分布列,然后求得期望。
的所有可能取值,分別求出概率后得到分布列,然后求得期望。
試題解析:
(1)由題意得列聯表為:
積極型 | 懈怠型 | 總計 | |
男 | 14 | 6 | 20 |
女 | 8 | 12 | 20 |
總計 | 22 | 18 | 40 |
由表中數據可得
![]() ,
,
故沒有95%以上的把握認為認為“評定類型”與“性別”有關.
(2)由條件知,從小王的微信好友中任選一人,其每日走路步數不超過![]() 步的概率為
步的概率為![]() ,超過
,超過![]() 步的概率為
步的概率為![]() .
.
由題意得![]() 的所有可能取值為0,1,2.
的所有可能取值為0,1,2.
![]() ,
,
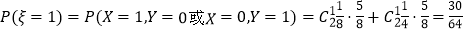 ,
,
![]()
故隨機變量![]() 的分布列為:
的分布列為:
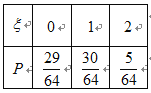
所以![]() .
.


 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】若AC⊥BC,AC=BC=1,點P是△ABC內一點,則![]() 的取值范圍是( )
的取值范圍是( )
A. (﹣![]() ,0) B. (0,
,0) B. (0,![]() ) C. (﹣
) C. (﹣![]() ,
,![]() ) D. (﹣1,1)
) D. (﹣1,1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一容量為50的樣本,數據的分組以及各組的頻數如下:
[12.5,15.5),3;[15.5,18.5),8;[18.5,21.5),9;[21.5,24.5),11;[24.5,27.5),10;[27.5,30.5),5;[30.5,33.5],4.
(1)列出樣本的頻率分布表.
(2)畫出頻率分布直方圖.
(3)根據頻率分布表,估計數據落在[15.5,24.5)內的可能性約是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解人們對“延遲退休年齡政策”的態度,某部門從年齡在![]() 歲到
歲到![]() 歲的人群中隨機調查了
歲的人群中隨機調查了![]() 人,并得到如圖所示的頻率分布直方圖,在這
人,并得到如圖所示的頻率分布直方圖,在這![]() 人中不支持“延遲退休年齡政策”的人數與年齡的統計結果如圖所示:
人中不支持“延遲退休年齡政策”的人數與年齡的統計結果如圖所示:

年齡 | 不支持“延遲退休年齡政策”的人數 |
|
|
|
|
|
|
|
|
|
|
(1)由頻率分布直方圖,估計這![]() 人年齡的平均數;
人年齡的平均數;
(2)根據以上統計數據填寫下面的![]() 列聯表,據此表,能否在犯錯誤的概率不超過
列聯表,據此表,能否在犯錯誤的概率不超過![]() 的前提下,認為以
的前提下,認為以![]() 歲為分界點的不同人群對“延遲退休年齡政策”的態度存在差異?
歲為分界點的不同人群對“延遲退休年齡政策”的態度存在差異?
45歲以下 | 45歲以上 | 總計 | |
不支持 | |||
支持 | |||
總計 |
附:![]()
參考數據:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某班學生喜愛打籃球是否與性別有關,對本班50人進行了問卷調查得到了如下的列聯表:
喜愛打籃球 | 不喜愛打籃球 | 合計 | |
男生 | 5 | ||
女生 | 10 | ||
合計 | 50 |
已知在全部50人中隨機抽取1人抽到喜愛打籃球的學生的概率為![]() .
.
(1)請將上面的列聯表補充完整;
(2)是否在犯錯誤的概率不超過0.5%的前提下認為喜愛打籃球與性別有關?說明你的理由.下面的臨界值表供參考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005] | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式:![]() ,其中
,其中![]() )
)![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖是A,B兩所學校藝術節期間收到的各類藝術作品的情況的統計圖:
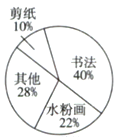

A學校 B學校
(1)從圖中能否看出哪所學校收到的水粉畫作品數量多?為什么?
(2)已知A學校收到的剪紙作品比B學校的多20件,收到的書法作品比B學校的少100件,請問這兩所學校收到藝術作品的總數分別是多少件?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市為了了解校園安全教育系列活動的成效,對全市高中生進行一次安全意識測試,根據測試成績評定“合格”、“不合格”兩個等級,同時對相應等級進行量化,現隨機抽取部分高中生的答卷,統計結果如下,對應的頻率分布直方圖如圖所示.
等級 | 不合格 | 合格 | ||
得分 | [20,40) | [40,60) | [60,80) | [80,100) |
頻數 | 12 |
| 48 | 24 |
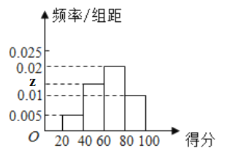
(1)求![]() 、
、![]() 的值;
的值;
(2)估計該市高中生測試成績評定等級為“合格”的概率;
(3)在抽取的答卷中,用分層抽樣的方法,從評定等級為“合格”和“不合格”的答卷中抽取5份,再從這5份答卷中任取2份,求恰有1份評定等級為“不合格”的概率
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com