
【題目】(本小題滿分12分)
某高校設計了一個實驗學科的實驗考查方案:考生從6道備選題中一次性隨機抽取3題,按照題目要求獨立完成全部實驗操作。規定:至少正確完成其中2題的便可提交通過。已知6道備選題中考生甲有4道題能正確完成,2道題不能完成;考生乙每題正確完成的概率都是![]() ,且每題正確完成與否互不影響。
,且每題正確完成與否互不影響。
(Ⅰ)分別寫出甲、乙兩考生正確完成題數的概率分布列,并計算數學期望;
(Ⅱ)試從兩位考生正確完成題數的數學期望及至少正確完成2題的概率分析比較兩位考生的實驗操作能力.
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),在以坐標原點為極點,
為參數),在以坐標原點為極點,![]() 軸的正半軸為極軸的極坐標系中,曲線
軸的正半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() (
(![]() 且
且![]() ).
).
(I)求直線![]() 的極坐標方程及曲線
的極坐標方程及曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)已知![]() 是直線
是直線![]() 上的一點,
上的一點,![]() 是曲線
是曲線![]() 上的一點,
上的一點, ![]() ,
,![]() ,若
,若![]() 的最大值為2,求
的最大值為2,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
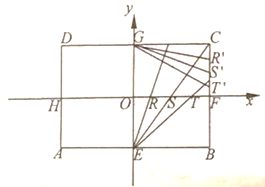
【題目】如圖,矩形ABCD中,![]() ,
,![]() ,E,F,G,H分別是矩形四條邊的中點,R,S,T是線段OF的四等分點,
,E,F,G,H分別是矩形四條邊的中點,R,S,T是線段OF的四等分點,![]() ,
,![]() ,
,![]() 是線段CF的四等分點,分別以HF,EG為x,y軸建立直角坐標系,設ER與
是線段CF的四等分點,分別以HF,EG為x,y軸建立直角坐標系,設ER與![]() ER與
ER與![]() 分別交于
分別交于![]() ,
,![]() ,ES與
,ES與![]() ES與
ES與![]() 交于
交于![]() ,
,![]() ,ET與
,ET與![]() 交于點N,則下列關于點
交于點N,則下列關于點![]() ,
,![]() ,
,![]() ,
,![]() ,N與兩個橢圓:
,N與兩個橢圓:![]() :
:![]() ,
,![]() :
:![]() 的位置關系敘述正確的是( )
的位置關系敘述正確的是( )
A.三點![]() ,
,![]() ,Nspan>在
,Nspan>在![]() ,點
,點![]() 在
在![]() 上B.
上B.![]() ,
,![]() 不在
不在![]() 上,
上,![]() ,N在
,N在![]() 上
上
C.點![]() 在
在![]() 上,點
上,點![]() ,
,![]() ,
,![]() 均不在
均不在![]() 上D.
上D.![]() ,
,![]() 在
在![]() 上,
上,![]() ,
,![]() 均不在
均不在![]() 上
上
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某籃球隊有![]() 名隊員,其中有
名隊員,其中有![]() 名隊員打前鋒,有
名隊員打前鋒,有![]() 名隊員打后衛,甲、乙兩名隊員既能打前鋒又能打后衛.若出場陣容為
名隊員打后衛,甲、乙兩名隊員既能打前鋒又能打后衛.若出場陣容為![]() 名前鋒,
名前鋒,![]() 名后衛,則不同的出場陣容共有______種.
名后衛,則不同的出場陣容共有______種.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著國內電商的不斷發展,快遞業也進入了高速發展時期,按照國務院的發展戰略布局,以及國家郵政管理總局對快遞業的宏觀調控,SF快遞收取快遞費的標準是:重量不超過1kg的包裹收費10元;重量超過1kg的包裹,在收費10元的基礎上,每超過1kg(不足1kg,按1kg計算)需再收5元.某縣SF分代辦點將最近承攬的100件包裹的重量統計如下:
重量(單位:kg) | (0,1] | (1,2] | (2,3] | (3,4] | (4,5] |
件數 | 43 | 30 | 15 | 8 | 4 |
對近60天,每天攬件數量統計如下表:
件數范圍 | 0~100 | 101~200 | 201~300 | 301~400 | 401~500 |
件數 | 50 | 150 | 250 | 350 | 450 |
天數 | 6 | 6 | 30 | 1 | 6 |
以上數據已做近似處理,將頻率視為概率.
(1)計算該代辦未來5天內不少于2天攬件數在101~300之間的概率;
(2)①估計該代辦點對每件包裹收取的快遞費的平均值;
②根據以往的經驗,該代辦點將快遞費的三分之一作為前臺工作人員的工資和公司利潤,其余的用作其他費用.目前該代辦點前臺有工作人員3人,每人每天攬件不超過150件,日工資110元.代辦點正在考慮是否將前臺工作人員裁減1人,試計算裁員前后代辦點每日利潤的數學期望,若你是決策者,是否裁減工作人員1人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場營銷人員對某商品![]() 進行市場營銷調查,發現每回饋消費者一定的點數,該商品每天的銷量就會發生一定的變化,經過統計得到下表:
進行市場營銷調查,發現每回饋消費者一定的點數,該商品每天的銷量就會發生一定的變化,經過統計得到下表:
回饋點數 | 1 | 2 | 3 | 4 | 5 |
銷量(百件)/天 | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)經分析發現,可用線性回歸模型擬合該商品每天的銷量![]() (百件)與返還點數
(百件)與返還點數![]() 之間的相關關系.請用最小二乘法求
之間的相關關系.請用最小二乘法求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并預測若回饋6個點時該商品每天銷量;
,并預測若回饋6個點時該商品每天銷量;
(2)已知節日期間某地擬購買該商品的消費群體十分龐大,營銷調研機構對其中的200名消費者的返點數額的心理預期值進行了抽樣調查,得到如下頻數表:
返還點數預期值區間 |
|
|
|
|
|
|
頻數 | 20 | 60 | 60 | 30 | 20 | 10 |
(i)求這200位擬購買該商品的消費者對返點點數的心理預期值的樣本平均數及中位數的估計值(同一區間的預期值可用該區間的中點值代替;估計值精確到0.1);
(ii)將對返點點數的心理預期值在![]() 和
和![]() 的消費者分別定義為“欲望緊縮型”消費者和“欲望膨脹型”消費者,現采用分層抽樣的方法從位于這兩個區間的30名消費者中隨機抽取6名,再從這6人中隨機抽取3名進行跟蹤調查,設抽出的3人中“欲望緊縮型”消費者的人數為隨機變量
的消費者分別定義為“欲望緊縮型”消費者和“欲望膨脹型”消費者,現采用分層抽樣的方法從位于這兩個區間的30名消費者中隨機抽取6名,再從這6人中隨機抽取3名進行跟蹤調查,設抽出的3人中“欲望緊縮型”消費者的人數為隨機變量![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
參考公式及數據:①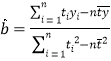 ,
,![]() ;②
;②![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 1左右焦點為F1,F2直線(
1左右焦點為F1,F2直線(![]() 1)x
1)x![]() y
y![]() 0與該橢圓有一個公共點在y軸上,另一個公共點的坐標為(m,1).
0與該橢圓有一個公共點在y軸上,另一個公共點的坐標為(m,1).
(1)求橢圓C的方程;
(2)設P為橢圓C上任一點,過焦點F1,F2的弦分別為PM,PN,設![]() λ1
λ1![]() λ2
λ2![]() ,求λ1+λ2的值.
,求λ1+λ2的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com