【題目】下列敘述錯誤的是（ ）
A.已知直線
和平面
，若點
，點
且
，
，則
B.若三條直線兩兩相交，則三條直線確定一個平面
C.若直線不平行于平面，且
，則內(nèi)的所有直線與都不相交
D.若直線
和
不平行，且
，
，
，則l至少與，中的一條相交
應(yīng)用題作業(yè)本系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】某早餐店對一款新口味的酸奶進行了一段時間試銷，定價為5元/瓶．酸奶在試銷售期間足量供應(yīng)，每天的銷售數(shù)據(jù)按照[15，25]，（25，35]，（35，45]，（45，55]分組，得到如下頻率分布直方圖，以不同銷量的頻率估計概率．試銷結(jié)束后，這款酸奶正式上市，廠家只提供整箱批發(fā)：大箱每箱50瓶，批發(fā)成本85元；小箱每箱30瓶，批發(fā)成本65元．由于酸奶保質(zhì)期短，當(dāng)天未賣出的只能作廢．該早餐店以試銷售期間的銷量作為參考，決定每天僅批發(fā)一箱（計算時每個分組取中間值作為代表，比如銷量為（45，55]時看作銷量為50瓶）．
（1）設(shè)早餐店批發(fā)一大箱時，當(dāng)天這款酸奶的利潤為隨機變量X，批發(fā)一小箱時，當(dāng)天這款酸奶的利潤為隨機變量Y，求X和Y的分布列；
（2）從早餐店的收益角度和利用所學(xué)的知識作為決策依據(jù)，該早餐店應(yīng)每天批發(fā)一大箱還是一小箱？（必須作出一種合理的選擇）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，四棱柱ABCD-A1B1C1D1中，CD∥AB, AB⊥BC,AB=BC=2CD=2,側(cè)棱AA1⊥平面ABCD.且點M是AB1的中點
(1)證明:CM∥平面ADD1A1；
(2)求點M到平面ADD1A1的距離.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
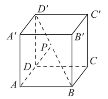
【題目】如圖所示,已知點P在正方體ABCD-A′B′C′D′的對角線BD′上,∠PDA=60°.
(1)求DP與CC′所成角的大小.
(2)求DP與平面AA′D′D所成角的大小.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】在
中，D，E，F分別是邊
，
，
中點，下列說法正確的是（ ）
A.
B.
C.若
，則
是
在
的投影向量
D.若點P是線段
上的動點，且滿足
，則
的最大值為
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，四棱錐
的底面
是菱形，且
，其對角線
、
交于點
， 
、
是棱
、
上的中點.
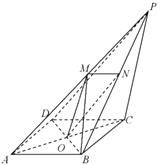
（1）求證：面
面
；
（2）若面
底面
， 
， 
， 
，求三棱錐
的體積.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)拋物線
的焦點為
，過點
的直線與拋物線相交于
兩點，與拋物線的準(zhǔn)線相交于點
， 
，則
與
的面積之比
__________．
【答案】
【解析】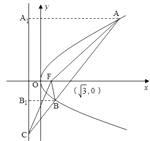
由題意可得拋物線的焦點
的坐標(biāo)為
，準(zhǔn)線方程為
。
如圖，設(shè)
，過A,B分別向拋物線的準(zhǔn)線作垂線，垂足分別為E,N，則
，解得
。
把
代入拋物線
，解得
。
∴直線AB經(jīng)過點
與點
，
故直線AB的方程為
，代入拋物線方程解得
。
∴
。
在
中， 
，
∴
∴
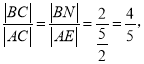
。答案： 
點睛：
在解決與拋物線有關(guān)的問題時，要注意拋物線的定義在解題中的應(yīng)用。拋物線定義有兩種用途：一是當(dāng)已知曲線是拋物線時，拋物線上的點M滿足定義，它到準(zhǔn)線的距離為d，則|MF|＝d，可解決有關(guān)距離、最值、弦長等問題；二是利用動點滿足的幾何條件符合拋物線的定義，從而得到動點的軌跡是拋物線．
【題型】填空題
【結(jié)束】
17
【題目】已知
三個內(nèi)角
所對的邊分別是
，若
.
（1）求角
；
（2）若
的外接圓半徑為2，求
周長的最大值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
