
【題目】已知![]() ,如圖,曲線
,如圖,曲線![]() 由曲線
由曲線![]() :
:![]() 和曲線
和曲線![]() :
:![]() 組成,其中點
組成,其中點![]() 為曲線
為曲線![]() 所在圓錐曲線的焦點,點
所在圓錐曲線的焦點,點![]() 為曲線
為曲線![]() 所在圓錐曲線的焦點.
所在圓錐曲線的焦點.
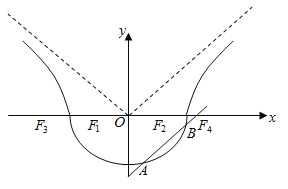
(Ⅰ)若![]() ,求曲線
,求曲線![]() 的方程;
的方程;
(Ⅱ)如圖,作直線![]() 平行于曲線
平行于曲線![]() 的漸近線,交曲線
的漸近線,交曲線![]() 于點
于點![]() ,求證:弦
,求證:弦![]() 的中點
的中點![]() 必在曲線
必在曲線![]() 的另一條漸近線上;
的另一條漸近線上;
(Ⅲ)對于(Ⅰ)中的曲線![]() ,若直線
,若直線![]() 過點
過點![]() 交曲線
交曲線![]() 于點
于點![]() ,求
,求![]() 面積的最大值.
面積的最大值.
【答案】(Ⅰ)![]() 和
和![]() .;(Ⅱ)證明見解析;(Ⅲ)
.;(Ⅱ)證明見解析;(Ⅲ)![]() .
.
【解析】
(Ⅰ)由![]() ,可得
,可得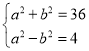 ,解出即可;
,解出即可;
(Ⅱ)設點![]() ,設直線
,設直線![]() ,與橢圓方程聯立可得:
,與橢圓方程聯立可得:![]() ,利用
,利用![]() ,根與系數的關系、中點坐標公式,證明即可;
,根與系數的關系、中點坐標公式,證明即可;
(Ⅲ)由(Ⅰ)知,曲線![]() ,且
,且![]() ,設直線
,設直線![]() 的方程為:
的方程為:![]() ,與橢圓方程聯立可得:
,與橢圓方程聯立可得:![]() ,利用根與系數的關系、弦長公式、三角形的面釈計算公式、基本不等式的性質,即可求解.
,利用根與系數的關系、弦長公式、三角形的面釈計算公式、基本不等式的性質,即可求解.
(Ⅰ)由題意:![]() ,
,
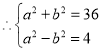 ,解得
,解得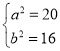 ,
,
則曲線![]() 的方程為:
的方程為:![]() 和
和![]() .
.
(Ⅱ)證明:由題意曲線![]() 的漸近線為:
的漸近線為:![]() ,
,
設直線![]() ,
,
則聯立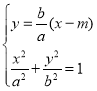 ,得
,得![]() ,
,
![]() ,解得:
,解得:![]() ,
,
又由數形結合知![]() .
.
設點![]() ,
,
則![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,即點
,即點![]() 在直線
在直線![]() 上.
上.
(Ⅲ)由(Ⅰ)知,曲線![]() ,點
,點![]() ,
,
設直線![]() 的方程為:
的方程為:![]() ,
,
![]() 聯立
聯立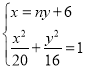 ,得:
,得:![]() ,
,
![]()
![]() ,
,
設![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 面積
面積![]() ,
,
令![]() ,
,![]() ,
,
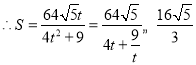
當且僅當![]() ,即
,即![]() 時等號成立,所以
時等號成立,所以![]() 面積的最大值為
面積的最大值為![]() .
.


科目:高中數學 來源: 題型:
【題目】
設函數![]()
(Ⅰ)若![]() 是函數
是函數![]() 的極值點,1和
的極值點,1和![]() 是
是![]() 的兩個不同零點,且
的兩個不同零點,且![]()
且![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若對任意![]() , 都存在
, 都存在![]() (
(![]() 為自然對數的底數),使得
為自然對數的底數),使得![]()
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (m
(m![]() R)的導函數為
R)的導函數為![]() .
.
(1)若函數![]() 存在極值,求m的取值范圍;
存在極值,求m的取值范圍;
(2)設函數![]() (其中e為自然對數的底數),對任意m
(其中e為自然對數的底數),對任意m![]() R,若關于x的不等式
R,若關于x的不等式![]() 在(0,
在(0,![]() )上恒成立,求正整數k的取值集合.
)上恒成立,求正整數k的取值集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,焦距為2,離心率
,焦距為2,離心率![]() 為
為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過點![]() 作圓
作圓![]() 的切線,切點分別為
的切線,切點分別為![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,過點
,過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,點
兩點,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,求
,求![]() 的面積的最大值.
的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年全國“兩會”,即中華人民共和國第十三屆全國人大二次會議和中國人民政治協商會議第十三屆全國委員會第二次會議,分別于2019年3月5日和3月3日在北京召開.為了了解哪些人更關注“兩會”,某機構隨機抽取了年齡在![]() 歲之間的200人進行調查.并按年齡繪制的頻率分布直方圖如圖所示,把年齡落在區間
歲之間的200人進行調查.并按年齡繪制的頻率分布直方圖如圖所示,把年齡落在區間![]() 和
和![]() 內的人分別稱為“青少年人”和“中老年人”
內的人分別稱為“青少年人”和“中老年人”![]() 經統計“青少年人”和“中老年人”的人數之比為
經統計“青少年人”和“中老年人”的人數之比為![]() ,其中“青少年人”中有40人關注“兩會”,“中老年人”中關注“兩會”和不關注“兩會”的人數之比是
,其中“青少年人”中有40人關注“兩會”,“中老年人”中關注“兩會”和不關注“兩會”的人數之比是![]() .
.
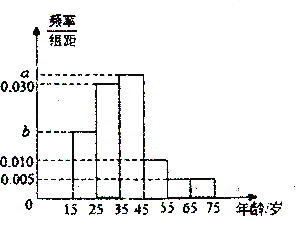
(1)求圖中a,b的值;
(2)現采用分層抽樣在![]() 和
和![]() 中隨機抽取8名代表,從8人中任選2人,求2人中至少有1個是“中老年人”的概率是多少?
中隨機抽取8名代表,從8人中任選2人,求2人中至少有1個是“中老年人”的概率是多少?
(3)根據已知條件,完成下面的![]() 列聯表,并根據此統計結果判斷:能否有
列聯表,并根據此統計結果判斷:能否有![]() 的把握認為“中老年人”比“青少年人”更加關注“兩會”?
的把握認為“中老年人”比“青少年人”更加關注“兩會”?
關注 | 不關注 | 合計 | |
青少年人 | |||
中老年人 | |||
合計 |
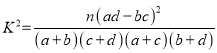
P(K2≥k0) | 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,已知PA⊥平面ABCD,且四邊形ABCD為直角梯形,∠ABC=∠BAD=![]() ,PA=AD=2,AB=BC=1,點M、E分別是PA、PD的中點
,PA=AD=2,AB=BC=1,點M、E分別是PA、PD的中點
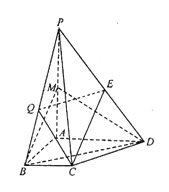
(1)求證:CE//平面BMD
(2)點Q為線段BP中點,求直線PA與平面CEQ所成角的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com