
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為:
的參數方程為: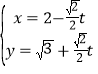 (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 與直線
與直線![]() 交于
交于![]() 兩點,若點
兩點,若點![]() 的坐標為
的坐標為![]() ,求
,求![]() .
.
 一線名師提優試卷系列答案
一線名師提優試卷系列答案科目:高中數學 來源: 題型:
【題目】2017年1月,《中國青年報》社會調查中心聯合問卷網,對多人進行了一項關于“二十四節氣”的調查,請選擇合適的圖表分別表示以下調查結果:
(1)全部都知道、大部分知道、少部分知道和完全不知道“二十四節氣”日期的受訪者分別占12.6%、49.0%、34.6%和3.8%;
(2)調查顯示,受訪者最敏感的節氣是立春(50.9%)、冬至(46.4%)和清明(43.9%).其他依次為:立冬(32.2%)、立秋(32.1%)、立夏(29.6%)、夏至(28.5%)、大暑(20.7%)、驚蟄(18.8%)、春分(18.7%)、雨水(18.7%)、大寒(16.4%)、大雪(15.3%)、秋分(14.8%)、小暑(14.0%)、芒種(12.2%)、小滿(11.6%)、處暑(11.6%)、白露(11.3%)、霜降(10.7%)和小雪(10.5%).最不敏感的節氣是谷雨(10.4%)、小寒(9.7%)和寒露(7.9%).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種商品價格與該商品日需求量之間的幾組對照數據如下表:
![]()
(1)求y關于x的線性回歸方程;
(2)利用(1)中的回歸方程,當價格x=40元/kg時,日需求量y的預測值為多少?
參考公式:線性回歸方程![]() ,其中
,其中![]() =
= ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別是
的左、右焦點分別是![]() ,其離心率
,其離心率![]() ,點
,點![]() 為橢圓上的一個動點,
為橢圓上的一個動點,![]() 面積的最大值為3.
面積的最大值為3.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)已知點![]() ,過點
,過點![]() 且斜率不為0的直線
且斜率不為0的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,直線
兩點,直線![]() ,
,![]() 與
與![]() 軸分別相交于
軸分別相交于![]() 兩點,試問
兩點,試問![]() 是否為定值?如果,求出這個定值;如果不是,請說明理由.
是否為定值?如果,求出這個定值;如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查某社區居民每天參加健身的時間,某機構在該社區隨機采訪男性、女性各50名,其中每人每天的健身時間不少于1小時稱為“健身族”,否則稱其為"非健身族”,調查結果如下:
健身族 | 非健身族 | 合計 | |
男性 | 40 | 10 | 50 |
女性 | 30 | 20 | 50 |
合計 | 70 | 30 | 100 |
(1)若居民每人每天的平均健身時間不低于70分鐘,則稱該社區為“健身社區”. 已知被隨機采訪的男性健身族,男性非健身族,女性健身族,女性非健身族每人每天的平均健分時間分別是1.2小時,0.8小時,1.5小時,0.7小時,試估計該社區可否稱為“健身社區”?
(2)根據以上數據,能否在犯錯誤的概率不超過5%的情況下認為“健身族”與“性別”有關?
參考公式: 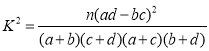 ,其中
,其中![]() .
.
參考數據:
| 0. 50 | 0. 40 | 0. 25 | 0. 05 | 0. 025 | 0. 010 |
| 0. 455 | 0. 708 | 1. 321 | 3. 840 | 5. 024 | 6. 635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家電公司銷售部門共有200位銷售員,每位部門對每位銷售員都有1400萬元的年度銷售任務,已知這200位銷售員去年完成銷售額都在區間![]() (單位:百萬元)內,現將其分成5組,第1組,第2組,第3組,第4組,第5組對應的區間分別為
(單位:百萬元)內,現將其分成5組,第1組,第2組,第3組,第4組,第5組對應的區間分別為![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,繪制出頻率分布直方圖.
,繪制出頻率分布直方圖.

(1)求![]() 的值,并計算完成年度任務的人數;
的值,并計算完成年度任務的人數;
(2)用分層抽樣從這200位銷售員中抽取容量為25的樣本,求這5組分別應抽取的人數;
(3)現從(2)中完成年度任務的銷售員中隨機選取2位,獎勵海南三亞三日游,求獲得此獎勵的2位銷售員在同一組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
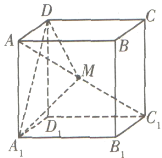
【題目】在棱長為1的正方體![]() 中,點
中,點![]() 是對角線
是對角線![]() 上的動點(點
上的動點(點![]() 與
與![]() 不重合),則下列結論正確的是____.
不重合),則下列結論正確的是____.
①存在點![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
②存在點![]() ,使得
,使得![]() 平面
平面![]() ;
;
③![]() 的面積不可能等于
的面積不可能等于![]() ;
;
④若![]() 分別是
分別是![]() 在平面
在平面![]() 與平面
與平面![]() 的正投影的面積,則存在點
的正投影的面積,則存在點![]() ,使得
,使得![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com