
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以坐標原點為極點,
為參數).以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若曲線![]() 上一點
上一點![]() 的極坐標為
的極坐標為![]() ,且
,且![]() 過點
過點![]() ,求
,求![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() ,
,![]() 與
與![]() 的交點為
的交點為![]() ,求
,求![]() 的最大值.
的最大值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,且
,且![]() 為自然對數的底數)
為自然對數的底數)
(1)判斷函數![]() 的單調性并證明;
的單調性并證明;
(2)判斷函數![]() 的奇偶性并證明;
的奇偶性并證明;
(3)是否存在實數![]() ,使不等式
,使不等式![]() 對一切
對一切![]() 都成立?若存在,求出
都成立?若存在,求出![]() 的范圍,若不存在說明理由.
的范圍,若不存在說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古希臘時期,人們認為最美人體的頭頂至肚臍的長度與肚臍至足底的長度之比是![]() (
(![]() ≈0.618,稱為黃金分割比例),著名的“斷臂維納斯”便是如此.此外,最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是
≈0.618,稱為黃金分割比例),著名的“斷臂維納斯”便是如此.此外,最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是![]() .若某人滿足上述兩個黃金分割比例,且腿長為105cm,頭頂至脖子下端的長度為26 cm,則其身高可能是
.若某人滿足上述兩個黃金分割比例,且腿長為105cm,頭頂至脖子下端的長度為26 cm,則其身高可能是

A. 165 cmB. 175 cmC. 185 cmD. 190cm
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]()
![]() 的離心率為
的離心率為![]() ,
,![]() ,
,![]() 分別為
分別為![]() 的右頂點和上頂點,且
的右頂點和上頂點,且![]() .
.
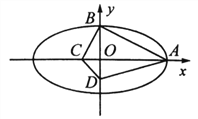
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若![]() ,
,![]() 分別是
分別是![]() 軸負半軸,
軸負半軸,![]() 軸負半軸上的點,且四邊形
軸負半軸上的點,且四邊形![]() 的面積為2,設直線
的面積為2,設直線![]() 和
和![]() 的交點為
的交點為![]() ,求點
,求點![]() 到直線
到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解學生的課外閱讀時間情況,某學校隨機抽取了 50人進行統計分析,把這50人每天閱讀的時間(單位:分鐘)繪制成頻數分布表,如下表所示:

若把每天閱讀時間在60分鐘以上(含60分鐘)的同學稱為“閱讀達人”,根據統計結果中男女生閱讀達人的數據,制作出如圖所示的等高條形圖.
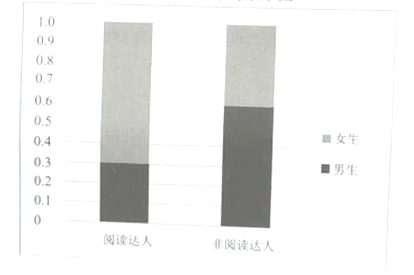
(1)根據抽樣結果估計該校學生的每天平均閱讀時間(同一組數據用該區間的中點值作為代表);
(2)根據已知條件完成下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為“閱讀達人”跟性別有關?
的把握認為“閱讀達人”跟性別有關?
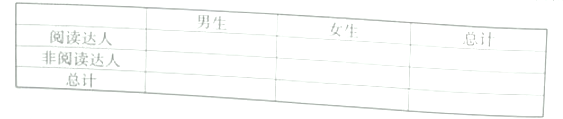
附:參考公式
![]() ,其中
,其中![]() .
.
臨界值表:
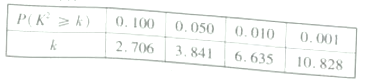
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的焦距為
的焦距為![]() ,離心率為
,離心率為![]() ,其右焦點為
,其右焦點為![]() ,過點
,過點![]() 作直線交橢圓于另一點
作直線交橢圓于另一點![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的面積;
的面積;
(Ⅱ)若過點![]() 的直線與橢圓
的直線與橢圓![]() 相交于兩點
相交于兩點![]() 、
、![]() ,設
,設![]() 為
為![]() 上一點,且滿足
上一點,且滿足![]() (
(![]() 為坐標原點),當
為坐標原點),當![]() 時,求實數
時,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l:mx﹣y=1,若直線l與直線x+m(m﹣1)y=2垂直,則m的值為_____,動直線l:mx﹣y=1被圓C:x2﹣2x+y2﹣8=0截得的最短弦長為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com