【題目】在△ABC中，角A、B、C的對邊分別為a、b、c，且
．
（1）求角A；
（2）若△ABC外接圓的面積為4π，且△ABC的面積
，求△ABC的周長．
【答案】（1）
．（2）
．
【解析】
(1)根據正弦定理邊化角,再利用三角函數和差角公式化簡求解即可.
(2)利用正弦定理可得
,再結合面積公式與余弦定理求解
即可.
解：（1）法一：已知
,由正弦定理得2sinAcosB＝2sinC﹣sinB＝2sin（A+B）﹣sinB,
可得：2cosAsinB﹣sinB＝0,可得：sinB（2cosA﹣1）＝0,
∵sinB≠0,
∴
,
∵A∈（0,π）,
∴
.
法二：已知,由余弦定理得
,可得：a2＝b2+c2﹣bc
又a2＝b2+c2﹣2bccosA,
∴,
∵A∈（0,π）,
∴.
（2）由△ABC外接圓的面積為πR2＝4π,得到R＝2,
由正弦定理知
,
∴.
∵△ABC的面積
,可得bc＝8.
法一：由余弦定理得a2＝b2+c2﹣2bccosA＝（b+c）2﹣3bc,即12＝（b+c）2﹣24
從而b+c＝6,故△ABC的周長為
.
法二：由余弦定理得a2＝b2+c2﹣2bccosA＝b2+c2﹣bc,即b2+c2＝20
從而
或
,
故△ABC的周長為.
海淀黃岡名師導航系列答案
普通高中同步練習冊系列答案科目：高中數學 來源： 題型：
【題目】一汽車廠生產
，
，
三類轎車，每類轎車均有舒適型和標準型兩種型號，某月的產量如下表(單位：輛)：按類用分層抽樣的方法在這個月生產的轎車中抽取50輛，其中有類轎車10輛．
轎車 | 轎車 | 轎車 | |
舒適型 | 100 | 150 |
|
標準型 | 300 | 450 | 600 |
（1）求
的值；
（2）用分層抽樣的方法在類轎車中抽取一個容量為5的樣本．將該樣本看成一個總體，從中任取2輛，求至少有1輛舒適型轎車的概率；
（3）用隨機抽樣的方法從類舒適型轎車中抽取8輛，經檢測它們的得分如下：9.4，8.6，9.2，9.6，8.7，9.3，9.0，8.2 把這8輛轎車的得分看作一個總體，從中任取一個得分數
，記這8輛轎車的得分的平均數為
，定義事件
，且函數
沒有零點
，求事件
發生的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
的焦點為
，點
在拋物線
上，
為坐標原點，
，且
.
（1）求拋物線的方程；
（2）圓
與拋物線順次交于
四點，
所在的直線
過焦點，線段
是圓的直徑，
，求直線的方程..
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某品牌手機廠商推出新款的旗艦機型，并在某地區跟蹤調查得到這款手機上市時間（第
周）和市場占有率（
）的幾組相關數據如下表：
|
|
|
|
|
|
|
|
|
|
|
|
（1）根據表中的數據，用最小二乘法求出
關于的線性回歸方程
；
（2）根據上述線性回歸方程，預測在第幾周，該款旗艦機型市場占有率將首次超過
（最后結果精確到整數）．
參考公式：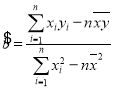
，
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數y＝f1（x），y＝f2（x），定義函數f（x）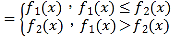
．
（1）設函數f1（x）＝x+3，f2（x）＝x2﹣x，求函數y＝f（x）的解析式；
（2）在（1）的條件下，g（x）＝mx+2（m∈R），函數h（x）＝f（x）﹣g（x）有三個不同的零點，求實數m的取值范圍；
（3）設函數f1（x）＝x2﹣2，f2（x）＝|x﹣a|，函數F（x）＝f1（x）+f2（x），求函數F（x）的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于正整數集合
，如果任意去掉其中一個元素
之后，剩余的所有元素組成的集合都能分為兩個交集為空集的集合，且這兩個集合的所有元素之和相等，就稱集合
為“可分集合”.
（1）判斷集合
和
是否是“可分集合”（不必寫過程）；
（2）求證：五個元素的集合
一定不是“可分集合”；
（3）若集合是“可分集合”.
①證明：
為奇數；
②求集合中元素個數的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
