
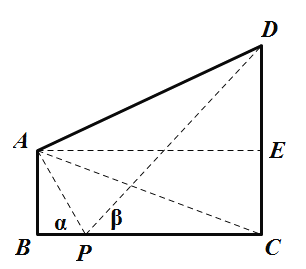
【題目】如圖,兩座建筑物AB,CD的底部都在同一個水平面上,且均與水平面垂直,它們的高度分別是10m和20m,從建筑物AB的頂部A看建筑物CD的視角∠CAD=60°.
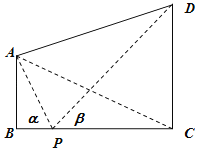
(1)求BC的長度;
(2)在線段BC上取一點P(點P與點B,C不重合),從點P看這兩座建筑物的視角分別為∠APB=α,∠DPC=β,問點P在何處時,α+β最小?
【答案】(1)![]() ;(2)當BP為
;(2)當BP為![]() cm時,α+β取得最小值.
cm時,α+β取得最小值.
【解析】
(1)作AE⊥CD,垂足為E,則CE=10,DE=10,設BC=x,根據![]() 得到
得到![]() ,解得答案.
,解得答案.
(2)設BP=t,則![]() ,故
,故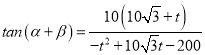 ,設
,設![]() ,求導得到函數單調性,得到最值.
,求導得到函數單調性,得到最值.
(1)作AE⊥CD,垂足為E,則CE=10,DE=10,設BC=x,
則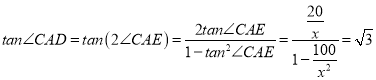 ,
,
化簡得![]() ,解之得,
,解之得,![]() 或
或![]() (舍),
(舍),
(2)設BP=t,則![]() ,
,
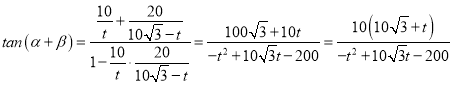 ,
,
設![]() ,
,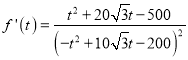 ,
,
令f'(t)=0,因為![]() ,得
,得![]() ,
,
當![]() 時,f'(t)<0,f(t)是減函數;
時,f'(t)<0,f(t)是減函數;
當![]() 時,f'(t)>0,f(t)是增函數,
時,f'(t)>0,f(t)是增函數,
所以,當![]() 時,f(t)取得最小值,即tan(α+β)取得最小值,
時,f(t)取得最小值,即tan(α+β)取得最小值,
因為![]() 恒成立,所以f(t)<0,
恒成立,所以f(t)<0,
所以tan(α+β)<0,![]() ,
,
因為y=tanx在![]() 上是增函數,所以當
上是增函數,所以當![]() 時,α+β取得最小值.
時,α+β取得最小值.


 海淀課時新作業金榜卷系列答案
海淀課時新作業金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 輕松課堂標準練系列答案
輕松課堂標準練系列答案科目:高中數學 來源: 題型:
【題目】某小學六年級學生的進行一分鐘跳繩檢測,現一班二班各有50人,根據檢測結果繪出了一班的頻數分布表和二班的頻率分布直方圖.
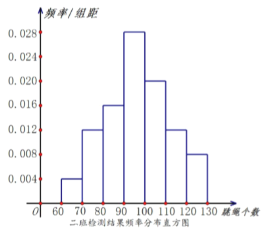
一班檢測結果頻數分布表:
跳繩個數區間 |
|
|
|
|
|
頻數 | 7 | 13 | 20 | 8 | 2 |
(1)根據給出的圖表估計一班和二班檢測結果的中位數(結果保留兩位小數);
(2)跳繩個數不小于100個為優秀,填寫下面2×2列聯表,并根據列聯表判斷是否有95%的把握認為檢測結果是否優秀與班級有關.
一班 | 二班 | 合計 | |
優秀 | |||
不優秀 | |||
合計 |
參考公式及數據: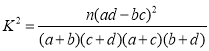 ,
,
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地有A,B、C、D四人先后感染了新型冠狀病毒,其中只有A到過疫區,B肯定是受A感染的,對于C,因為難以判定他是受A還是受B感染的,于是假定他受A和受B感染的概率都是![]() ,同樣也假設D受A、B和C感染的概率都是
,同樣也假設D受A、B和C感染的概率都是![]() .在這種假定之下,B、C、D中直接受A感染的人數X就是一個隨機變量,寫出X的可能取值為______,并求X的均值(即數學期望)為______.
.在這種假定之下,B、C、D中直接受A感染的人數X就是一個隨機變量,寫出X的可能取值為______,并求X的均值(即數學期望)為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種賭博每局的規則是:賭客先在標記有1,2,3,4,5的卡片中隨機摸取一張,將卡片上的數字作為其賭金;隨后放回該卡片,再隨機摸取兩張,將這兩張卡片上數字之差的絕對值的1.4倍作為其獎金.若隨機變量ξ1和ξ2分別表示賭客在一局賭博中的賭金和獎金,則D(ξ1)=_____,E(ξ1)﹣E(ξ2)=_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某車間4小時內生產了100根不同規格的三角鋼材(單位:厘米),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分組的頻率分布直方圖如圖.
分組的頻率分布直方圖如圖.
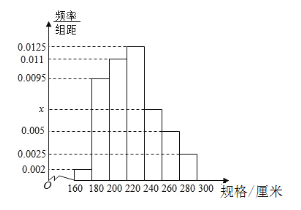
(1)求直方圖中![]() 的值;
的值;
(2)求這批鋼材規格的眾數;
(3)在規格為![]() ,
,![]() ,
,![]() ,
,![]() 的四組鋼材中,用分層抽樣的方法抽取11根鋼材,則在
的四組鋼材中,用分層抽樣的方法抽取11根鋼材,則在![]() 的規格中應抽取多少根?
的規格中應抽取多少根?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代的數學名著,書中把三角形的田稱為“圭田”,把直角梯形的田稱為“邪田”,稱底是“廣”,稱高是“正從”,“步”是丈量土地的單位.現有一邪田,廣分別為十步和二十步,正從為十步,其內有一塊廣為八步,正從為五步的圭田.若在邪田內隨機種植一株茶樹,求該株茶樹恰好種在圭田內的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C的參數方程為![]() (t為參數),以原點O為極點,x軸的非負半軸為極軸建立極坐標系,過極點的兩射線
(t為參數),以原點O為極點,x軸的非負半軸為極軸建立極坐標系,過極點的兩射線![]() 、
、![]() 相互垂直,與曲線C分別相交于A、B兩點(不同于點O),且
相互垂直,與曲線C分別相交于A、B兩點(不同于點O),且![]() 的傾斜角為銳角
的傾斜角為銳角![]() .
.
(1)求曲線C和射線![]() 的極坐標方程;
的極坐標方程;
(2)求△OAB的面積的最小值,并求此時![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型娛樂場有兩種型號的水上摩托,管理人員為了了解水上摩托的使用情況及給娛樂城帶來的經濟收入情況,對該場所最近6年水上摩托的使用情況進行了統計,得到相關數據如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代碼x | 1 | 2 | 3 | 4 | 5 | 6 |
使用率 | 11 | 13 | 16 | 15 | 20 | 21 |
(Ⅰ)請根據以上數據,用最小二乘法求水上摩托使用率![]() 關于年份代碼
關于年份代碼![]() 的線性回歸方程,并預測該娛樂場2019年水上摩托的使用率;
的線性回歸方程,并預測該娛樂場2019年水上摩托的使用率;
(Ⅱ)隨著生活水平的提高,外出旅游的老百姓越來越多,該娛樂場根據自身發展需求,準備重新進購一批水上摩托,其型號主要是目前使用的Ⅰ型、Ⅱ型兩種,每輛價格分別為1萬元、![]() 萬元.根據以往經驗,每輛水上摩托的的使用年限不超過四年.娛樂場管理部對已經淘汰的兩款水上摩托的使用情況分別抽取了50輛進行統計,使用年限如條形圖所示:
萬元.根據以往經驗,每輛水上摩托的的使用年限不超過四年.娛樂場管理部對已經淘汰的兩款水上摩托的使用情況分別抽取了50輛進行統計,使用年限如條形圖所示:
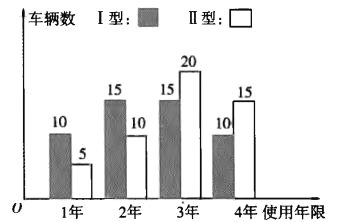
已知每輛水上摩托從購入到淘汰平均年收益是![]() 萬元,若用頻率作為概率,以每輛水上摩托純利潤(純利潤=收益-購買成本)的期望值為參考值,則該娛樂場的負責人應選哪種型號的水上摩托?
萬元,若用頻率作為概率,以每輛水上摩托純利潤(純利潤=收益-購買成本)的期望值為參考值,則該娛樂場的負責人應選哪種型號的水上摩托?
附:線性回歸方程為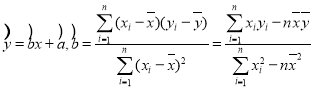 ,
,![]() ,
,
參考數據:![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com