
【題目】在如圖所示的圓臺中,AC是下底面圓O的直徑,EF是上底面圓O′的直徑,FB是圓臺的一條母線. 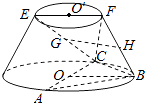
(1)已知G,H分別為EC,FB的中點,求證:GH∥平面ABC;
(2)已知EF=FB= ![]() AC=2
AC=2 ![]() ,AB=BC,求二面角F﹣BC﹣A的余弦值.
,AB=BC,求二面角F﹣BC﹣A的余弦值.
【答案】
(1)證明:取FC中點Q,連結GQ、QH,
∵G、H為EC、FB的中點,
∴GQ ![]()
![]() ,QH
,QH ![]()
![]() ,
,
又∵EF∥BO,∴GQ∥BO,
∴平面GQH∥平面ABC,
∵GH面GQH,∴GH∥平面ABC.
(2)解:∵AB=BC,∴BO⊥AC,
又∵OO′⊥面ABC,
∴以O為原點,OA為x軸,OB為y軸,OO′為z軸,建立空間直角坐標系,
則A( ![]() ,0,0),C(﹣2
,0,0),C(﹣2 ![]() ,0,0),B(0,2
,0,0),B(0,2 ![]() ,0),O′(0,0,3),F(0,
,0),O′(0,0,3),F(0, ![]() ,3),
,3),
![]() =(﹣2
=(﹣2 ![]() ,﹣
,﹣ ![]() ,﹣3),
,﹣3), ![]() =(2
=(2 ![]() ,2
,2 ![]() ,0),
,0),
由題意可知面ABC的法向量為 ![]() =(0,0,3),
=(0,0,3),
設 ![]() =(x0,y0,z0)為面FCB的法向量,
=(x0,y0,z0)為面FCB的法向量,
則 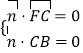 ,即
,即 ![]() ,
,
取x0=1,則 ![]() =(1,﹣1,﹣
=(1,﹣1,﹣ ![]() ),
),
∴cos< ![]() ,
, ![]() >=
>= 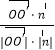 =﹣
=﹣ ![]() .
.
∵二面角F﹣BC﹣A的平面角是銳角,
∴二面角F﹣BC﹣A的余弦值為 ![]() .
.
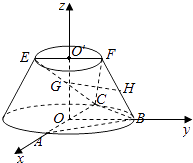
【解析】(1)取FC中點Q,連結GQ、QH,推導出平面GQH∥平面ABC,由此能證明GH∥平面ABC.(2)由AB=BC,知BO⊥AC,以O為原點,OA為x軸,OB為y軸,OO′為z軸,建立空間直角坐標系,利用向量法能求出二面角F﹣BC﹣A的余弦值.


 快捷英語周周練系列答案
快捷英語周周練系列答案科目:高中數學 來源: 題型:
【題目】已知2件次品和3件正品混放在一起,現需要通過檢測將其區分,每次隨機檢測一件產品,檢測后不放回,直到檢測出2件次品或者檢測出3件正品時檢測結束.
(1)求最后取出的是正品的概率;
(2)已知每檢測一件產品需要費用100元,設![]() 表示直到檢測出2件次品或者檢測出3件正品時所需要的檢測費用(單位:元),求
表示直到檢測出2件次品或者檢測出3件正品時所需要的檢測費用(單位:元),求![]() 的分布列和數學期望
的分布列和數學期望
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】通過隨機詢問100性別不同的大學生是否愛好某項運動,得到如下2×2列聯表:
男 | 女 | 總計 | |
愛好 | 40 | ||
不愛好 | 25 | ||
總計 | 45 | 100 |
(1)將題中的2×2列聯表補充完整;
(2)能否有99%的把握認為斷愛好該項運動與性別有關?請說明理由;
附:K2= ![]() ,
,
p(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
(3)利用分層抽樣的方法從以上愛好該項運動的大學生中抽取6人組建了“運動達人社”,現從“運動達人設”中選派3人參加某項校際挑戰賽,記選出3人中的女大學生人數為X,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=|x+1|﹣|2x﹣4|;
(1)解不等式f(x)≥1;
(2)若對x∈R,都有f(x)+3|x﹣2|>m,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設a,b∈R,c∈[0,2π),若對任意實數x都有2sin(3x﹣ ![]() )=asin(bx+c),定義在區間[0,3π]上的函數y=sin2x的圖象與y=cosx的圖象的交點個數是d個,則滿足條件的有序實數組(a,b,c,d)的組數為( )
)=asin(bx+c),定義在區間[0,3π]上的函數y=sin2x的圖象與y=cosx的圖象的交點個數是d個,則滿足條件的有序實數組(a,b,c,d)的組數為( )
A.7
B.11
C.14
D.28
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某家庭記錄了未使用節水龍頭50天的日用水量數據(單位:m3)和使用了節水龍頭50天的日用水量數據,得到頻數分布表如下:
未使用節水龍頭50天的日用水量頻數分布表
日用 水量 | [0,0.1) | [0.1,0.2) | [0.2,0.3) | [0.3,0.4) | [0.4,0.5) | [0.5,0.6) | [0.6,0.7) |
頻數 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了節水龍頭50天的日用水量頻數分布表
日用 水量 | [0,0.1) | [0.1,0.2) | [0.2,0.3) | [0.3,0.4) | [0.4,0.5) | [0.5,0.6) |
頻數 | 1 | 5 | 13 | 10 | 16 | 5 |
⑴在答題卡上作出使用了節水龍頭
⑵估計該家庭使用節水龍頭后,日用水量小于0.35m3的概率;
⑶估計該家庭使用節水龍頭后,一年能節省多少水?(一年按365天計算,同一組中的數據以這組數據所在區間中點的值作代表.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的極坐標方程是
的極坐標方程是![]() .以極點為平面直角坐標系的原點,極軸為
.以極點為平面直角坐標系的原點,極軸為![]() 軸的正半軸,建立平面直角坐標系,直線
軸的正半軸,建立平面直角坐標系,直線![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數).
為參數).
(Ⅰ)將曲線![]() 的極坐標方程化為直角坐標方程;
的極坐標方程化為直角坐標方程;
(Ⅱ)若直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的傾斜角
的傾斜角![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在![]() 上的函數
上的函數 ![]() 和
和![]() 的圖象如圖
的圖象如圖


給出下列四個命題:
①方程![]() 有且僅有
有且僅有![]() 個根;②方程
個根;②方程![]() 有且僅有
有且僅有![]() 個根;
個根;
③方程![]() 有且僅有
有且僅有![]() 個根;④方程
個根;④方程![]() 有且僅有
有且僅有![]() 個根;
個根;
其中正確命題的序號是( )
A. ①②③ B. ②③④ C. ①②④ D. ①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新能源汽車的春天來了!2018年3月5日上午,李克強總理做政府工作報告時表示,將新能源汽車車輛購置稅優惠政策再延長三年,自2018年1月1日至2020年12月31日,對購置的新能源汽車免征車輛購置稅.某人計劃于2018年5月購買一輛某品牌新能源汽車,他從當地該品牌銷售網站了解到近五個月實際銷量如下表:
月份 | 2017.12 | 2018.01 | 2018.02 | 2018.03 | 2018.04 |
月份編號t | 1 | 2 | 3 | 4 | 5 |
銷量(萬輛) | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)經分析,可用線性回歸模型擬合當地該品牌新能源汽車實際銷量![]() (萬輛)與月份編號
(萬輛)與月份編號![]() 之間的相關關系.請用最小二乘法求
之間的相關關系.請用最小二乘法求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并預測2018年5月份當地該品牌新能源汽車的銷量;
,并預測2018年5月份當地該品牌新能源汽車的銷量;
(2)2018年6月12日,中央財政和地方財政將根據新能源汽車的最大續航里程(新能源汽車的最大續航里程是指理論上新能源汽車所裝的燃料或電池所能夠提供給車跑的最遠里程)對購車補貼進行新一輪調整.已知某地擬購買新能源汽車的消費群體十分龐大,某調研機構對其中的200名消費者的購車補貼金額的心理預期值進行了一個抽樣調查,得到如下一份頻數表:
補貼金額預期值區間(萬元) |
|
|
|
|
|
|
20 | 60 | 60 | 30 | 20 | 10 |
將頻率視為概率,現用隨機抽樣方法從該地區擬購買新能源汽車的所有消費者中隨機抽取3人,記被抽取3人中對補貼金額的心理預期值不低于3萬元的人數為![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
參考公式及數據:①回歸方程![]() ,其中
,其中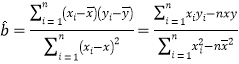 ,
,![]() ,②
,②![]() ,.
,.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com