
【題目】如圖,AC是圓O的直徑,點B在圓O上,∠BAC=30°,BM⊥AC于點M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.

(1)證明:EM⊥BF;
(2)求平面BEF與平面ABC所成的銳二面角的余弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】試題分析:(1)要證線線垂直,一般是用線面垂直的性質定理,先證線面垂直,本題從圖中看,想象能不能證明![]() ,為此要證
,為此要證![]() ,對
,對![]() ,因為
,因為![]() 是
是![]() 在平面
在平面![]() 上的射影,且
上的射影,且![]() ,從而有
,從而有![]() ,對
,對![]() ,可通過求出
,可通過求出![]() 的三邊長,由勾股定理得結論;當然結合第(2)小題求二面角,我們還可以以A為坐標原點,過點A垂直于AC的直線為x軸,AC、AE所在的直線分別為y、z軸建立空間直角坐標系.通過向量法證明線線垂直,(2)通過二面角的兩個面的法向量來求得二面角.
的三邊長,由勾股定理得結論;當然結合第(2)小題求二面角,我們還可以以A為坐標原點,過點A垂直于AC的直線為x軸,AC、AE所在的直線分別為y、z軸建立空間直角坐標系.通過向量法證明線線垂直,(2)通過二面角的兩個面的法向量來求得二面角.
試題解析:(1)證法一:![]() ,
,![]() ,又∵BM⊥AC,
,又∵BM⊥AC,![]()
![]() ①
①
而![]()
![]() ,
,![]() ,
,
即![]()
∴![]() ②
②![]() ③
③
由①②③得![]() ,∴EM⊥BF
,∴EM⊥BF
證法二:在Rt△ABC中,AC=4,∠BAC=30°
∴AB=2![]() ,BC=2,又BM⊥AC
,BC=2,又BM⊥AC
則AM=3,BM=![]() .
.
如圖,以A為坐標原點,過點A垂直于AC的直線為x軸,AC、AE所在的直線分別為y、z軸
建立空間直角坐標系.
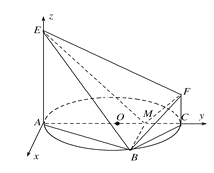
由已知條件得A(0,0,0),M(0,3,0),E(0,0,3),B(![]() ,3,0),F(0,4,1),
,3,0),F(0,4,1),
∴![]() =(0,-3,3),
=(0,-3,3),![]() =(-
=(-![]() ,1,1).
,1,1).
由![]() ·
·![]() =(0,-3,3)·(-
=(0,-3,3)·(-![]() ,1,1)=0,
,1,1)=0,
得![]() ⊥
⊥![]() ,∴EM⊥BF.
,∴EM⊥BF.
(2)解:由(1)知![]() =(-
=(-![]() ,-3,3),
,-3,3),![]() =(-
=(-![]() ,1,1).
,1,1).
設平面BEF的法向量為n=(x,y,z),
由n·![]() =0,n·
=0,n·![]() =0,得
=0,得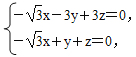
令x=![]() 得y=1,z=2,∴n=(
得y=1,z=2,∴n=(![]() ,1,2),
,1,2),
由已知EA⊥平面ABC,
所以取面ABC的法向量為![]() =(0,0,3),
=(0,0,3),
設平面BEF與平面ABC所成的銳二面角為θ,
則![]() ,
,
平面BEF與平面ABC所成的銳二面角的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex-ax2(x∈R),e=2.718 28…為自然對數的底數.
(1)求函數f(x)在點P(0,1)處的切線方程;
(2)若函數f(x)為R上的單調遞增函數,試求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)是定義域為R的周期函數,最小正周期為2,且
f(1+x)=f(1-x),當-1≤x≤0時,f(x)=-x.
(1)判斷f(x)的奇偶性;
(2)試求出函數f(x)在區間[-1,2]上的表達式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在(0,+∞)上的單調函數f(x),x∈(0,+∞),f[f(x)﹣lnx]=1,則方程f(x)﹣f′(x)=1的解所在區間是 ( )
A. (2,3) B. ![]() C.
C. ![]() D. (1,2)
D. (1,2)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 圖象上不同兩點
圖象上不同兩點![]() ,
, ![]() 處切線的斜率分別是
處切線的斜率分別是![]() ,
, ![]() ,規定
,規定![]() (
(![]() 為線段
為線段![]() 的長度)叫做曲線
的長度)叫做曲線![]() 在點
在點![]() 與
與![]() 之間的“彎曲度”,給出以下命題:
之間的“彎曲度”,給出以下命題:
①函數![]() 圖象上兩點
圖象上兩點![]() 與
與![]() 的橫坐標分別為1和2,則
的橫坐標分別為1和2,則![]() ;
;
②存在這樣的函數,圖象上任意兩點之間的“彎曲度”為常數;
③設點![]() ,
, ![]() 是拋物線
是拋物線![]() 上不同的兩點,則
上不同的兩點,則![]() ;
;
④設曲線![]() (
(![]() 是自然對數的底數)上不同兩點
是自然對數的底數)上不同兩點![]() ,
, ![]() ,且
,且![]() ,若
,若![]() 恒成立,則實數
恒成立,則實數![]() 的取值范圍是
的取值范圍是![]() .
.
其中真命題的序號為__________.(將所有真命題的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市隨機抽取一年(365天)內100天的空氣質量指數![]() (Air Pollution Index)的監測數據,結果統計如下:
(Air Pollution Index)的監測數據,結果統計如下:
|
|
|
|
|
|
| 大于300 |
空氣質量 | 優 | 良 | 輕微污染 | 輕度污染 | 中度污染 | 中度重 污染 | 重度污染 |
天數 | 10 | 15 | 20 | 30 | 7 | 6 | 12 |
(Ⅰ)若本次抽取的樣本數據有30天是在供暖季,其中有7天為重度污染,完成下面![]() 列聯表,并判斷能否有
列聯表,并判斷能否有![]() 的把握認為該市本年空氣重度污染與供暖有關?
的把握認為該市本年空氣重度污染與供暖有關?
非重度污染 | 重度污染 | 合計 | |
供暖季 | |||
非供暖季 | |||
合計 | 100 |
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 5.024 | 6.635 | 7.879 | 10.828 |
附: 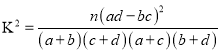
(Ⅱ)政府要治理污染,決定對某些企業生產進行管控,當![]() 在區間
在區間![]() 時企業正常生產;當
時企業正常生產;當![]() 在區間
在區間![]() 時對企業限產
時對企業限產![]() (即關閉
(即關閉![]() 的產能),當
的產能),當![]() 在區間
在區間![]() 時對企業限產
時對企業限產![]() ,當
,當![]() 在300以上時對企業限產
在300以上時對企業限產![]() ,企業甲是被管控的企業之一,若企業甲正常生產一天可得利潤2萬元,若以頻率當概率,不考慮其他因素:
,企業甲是被管控的企業之一,若企業甲正常生產一天可得利潤2萬元,若以頻率當概率,不考慮其他因素:
①在這一年中隨意抽取5天,求5天中企業被限產達到或超過![]() 的恰為2天的概率;
的恰為2天的概率;
②求企業甲這一年因限產減少的利潤的期望值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知直線
中,已知直線![]() 與橢圓
與橢圓![]() 交于點
交于點![]() ,
, ![]() (
(![]() 在
在![]() 軸上方),且
軸上方),且![]() .設點
.設點![]() 在
在![]() 軸上的射影為
軸上的射影為![]() ,三角形
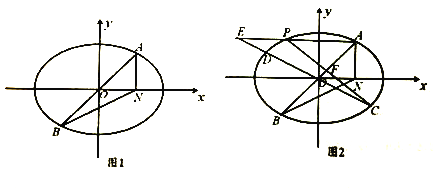
,三角形![]() 的面積為2(如圖1).
的面積為2(如圖1).
(1)求橢圓的方程;
(2)設平行于![]() 的直線與橢圓相交,其弦的中點為
的直線與橢圓相交,其弦的中點為![]() .
.
①求證:直線![]() 的斜率為定值;
的斜率為定值;
②設直線![]() 與橢圓相交于兩點
與橢圓相交于兩點![]() ,
, ![]() (
(![]() 在
在![]() 軸上方),點
軸上方),點![]() 為橢圓上異于
為橢圓上異于![]() ,
, ![]() ,
, ![]() ,
, ![]() 一點,直線
一點,直線![]() 交
交![]() 于點
于點![]() ,
, ![]() 交
交![]() 于點
于點![]() ,如圖2,求證:
,如圖2,求證: ![]() 為定值.
為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com