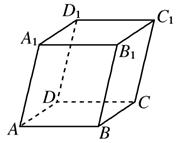
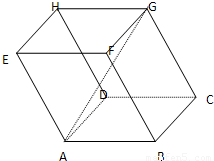
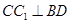分析:(1)連接BO,取DO中點H,連接GH,由題意可得:平面AD1⊥平面AC,進而證明BO⊥平面AD1,由GH與OB的關系可得答案.
(2)建立空間直角坐標系,根據題意分別求出兩個平面的法向量,結合向量間的運算關系求出兩個向量的夾角.進而轉化為二面角的平面角.
解答: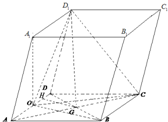
解:(1)連接BO,取DO中點H,連接GH,
因為A
1O⊥平面AC,所以平面AD
1⊥平面AC,
又底面為菱形,O為AD中點,
所以BO⊥平面AD
1,
因為GH∥BO,
所以GH⊥平面AD
1,
又GH=
BD=
,
所以點G到平面ADD
1A
1的距離為
.
(2)分別以OA,OB,OA
1所在直線為x,y,z軸,建立如圖所示的坐標系,
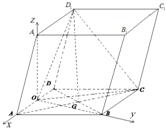
則
G(-,,0),D
1(-2,0,a),所以
=(,,-a),
面AD
1的一個法向量
n=(0,,0),
所以
cos?n,>==,解得a=1,
因為面OCD的一個法向量為n=(0,0,1),
設面OCD
1的一個法向量為p=(x,y,z),則
=(-2,0,1),
=(-2,,0),
則有
所以
,
取
x=,
m=(,2,2),
則
cos<p,m>==,
所以二面角D-OC-D
1的大小為
arccos.
點評:夾角成立問題的關鍵是數列掌握幾何體的結構特征,以便得到線面關系以及建立坐標系,利用向量夾角空間角,空間距離等問題.

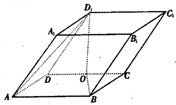
 如圖,平行六面體ABCD-A1B1C1D1中,底面ABCD是邊長為2的菱形,∠BAD=
如圖,平行六面體ABCD-A1B1C1D1中,底面ABCD是邊長為2的菱形,∠BAD= 解:(1)連接BO,取DO中點H,連接GH,
解:(1)連接BO,取DO中點H,連接GH, 則 G(-
則 G(-

 如圖,平行六面體ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,頂點D1在底面ABCD上的射影O恰好是CD的中點.
如圖,平行六面體ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,頂點D1在底面ABCD上的射影O恰好是CD的中點.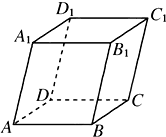 如圖,平行六面體ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,
如圖,平行六面體ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,