
【題目】某網購平臺為了解某市居民在該平臺的消費情況,從該市使用其平臺且每周平均消費額超過100元的人員中隨機抽取了100名,并繪制如圖所示頻率分布直方圖,已知中間三組的人數可構成等差數列.
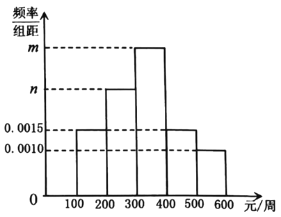
(1)求![]() 的值;
的值;
(2)分析人員對100名調查對象的性別進行統計發現,消費金額不低于300元的男性有20人,低于300元的男性有25人,根據統計數據完成下列![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為消費金額與性別有關?
的把握認為消費金額與性別有關?
(3)分析人員對抽取對象每周的消費金額![]() 與年齡
與年齡![]() 進一步分析,發現他們線性相關,得到回歸方程
進一步分析,發現他們線性相關,得到回歸方程![]() .已知100名使用者的平均年齡為38歲,試判斷一名年齡為25歲的年輕人每周的平均消費金額為多少.(同一組數據用該區間的中點值代替)
.已知100名使用者的平均年齡為38歲,試判斷一名年齡為25歲的年輕人每周的平均消費金額為多少.(同一組數據用該區間的中點值代替)
![]() 列聯表
列聯表
男性 | 女性 | 合計 | |
消費金額 | |||
消費金額 | |||
合計 |
臨界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
![]() ,其中
,其中![]()
【答案】(1)![]() ,
,![]() (2)詳見解析(3)395元
(2)詳見解析(3)395元
【解析】
(1)根據頻率分布直方圖可得![]() ,結合
,結合![]() 可得
可得![]() 的值.
的值.
(2)根據表格數據可得![]() ,再根據臨界值表可得有
,再根據臨界值表可得有![]() 的把握認為消費金額與性別有關.
的把握認為消費金額與性別有關.
(3)由頻率分布直方圖可得調查對象的周平均消費,從而得到![]() ,利用線性回歸方程可計算年齡為25歲的年輕人每周的平均消費金額.
,利用線性回歸方程可計算年齡為25歲的年輕人每周的平均消費金額.
(1)由頻率分布直方圖可知,![]() ,
,
由中間三組的人數成等差數列可知![]() ,
,
可解得![]() ,
,![]()
(2)周平均消費不低于300元的頻率為![]() ,因此100人中,周平均消費不低于300元的人數為
,因此100人中,周平均消費不低于300元的人數為![]() 人.
人.
所以![]() 列聯表為
列聯表為
男性 | 女性 | 合計 | |
消費金額 | 20 | 40 | 60 |
消費金額 | 25 | 15 | 40 |
合計 | 45 | 55 | 100 |
![]()
所以有![]() 的把握認為消費金額與性別有關.
的把握認為消費金額與性別有關.
(3)調查對象的周平均消費為
![]() ,
,
由題意![]() ,∴
,∴![]()
![]() .
.
∴該名年齡為25歲的年輕人每周的平均消費金額為395元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某高校共有學生15000人,其中男生10500人,女生4500人,為調查該校學生每周平均體育運動時間的情況,采用分層抽樣的方法,收集300位學生每周平均體育運動時間的樣本數據(單位:小時).
(1)應收集多少位女生樣本數據?
(2)根據這300個樣本數據,得到學生每周平均體育運動時間的頻率分布直方圖(如圖所示),其中樣本數據分組區間為:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .估計該校學生每周平均體育運動時間超過6個小時的概率.
.估計該校學生每周平均體育運動時間超過6個小時的概率.
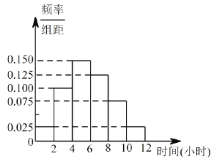
(3)在樣本數據中,有60位女生的每周平均體育運動時間超過4個小時.請完成每周平均體育運動時間與性別的列聯表,并判斷是否有95%的把握認為“該校學生的每周平均體育運動時間與性別有關”.
|
|
|
|
|
|
|
|
|
|
附: .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是__________(填序號)
(1)已知相關變量![]() 滿足回歸方程
滿足回歸方程![]() ,若變量
,若變量![]() 增加一個單位,則
增加一個單位,則![]() 平均增加
平均增加![]() 個單位
個單位
(2)若![]() 為兩個命題,則“
為兩個命題,則“![]() ”為假命題是“
”為假命題是“![]() ”為假命題的充分不必要條件
”為假命題的充分不必要條件
(3)若命題![]() ,
,![]() ,則
,則![]() ,
,![]()
(4)已知隨機變量![]() ,若
,若![]() ,則
,則![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國于2015年10月宣布實施普遍二孩政策,為了解戶籍、性別對生育二胎選擇傾向的影響,某地從育齡群體中隨機抽取了容量為140的調查樣本,其中城鎮戶籍與農村戶籍各70人;男性60人,女性80人,繪制的不同群體中傾向選擇生育二胎與傾向選擇不生育二胎的人數比例如圖所示,其中陰影部分表示傾向選擇生育二胎的對應比例,則下列敘述正確的是( )
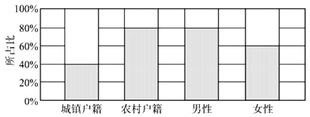
A.是否傾向選擇生育二胎與戶籍有關
B.是否傾向選擇生育二胎與性別有關
C.調查樣本里面傾向選擇生育二胎的人群中,男性人數少于女性人數
D.傾向選擇不生育二胎的人群中,農村戶籍人數多于城鎮戶籍人數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本題16分)某鄉鎮為了進行美麗鄉村建設,規劃在長為10千米的河流OC的一側建一條觀光帶,觀光帶的前一部分為曲線段OAB,設曲線段OAB為函數![]() ,
,![]() (單位:千米)的圖象,且曲線段的頂點為
(單位:千米)的圖象,且曲線段的頂點為![]() ;觀光帶的后一部分為線段BC,如圖所示.
;觀光帶的后一部分為線段BC,如圖所示.
(1)求曲線段OABC對應的函數![]() 的解析式;
的解析式;
(2)若計劃在河流OC和觀光帶OABC之間新建一個如圖所示的矩形綠化帶MNPQ,綠化帶由線段MQ,QP, PN構成,其中點P在線段BC上.當OM長為多少時,綠化帶的總長度最長?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某種螺帽是由一個半徑為2的半球體挖去一個正三棱錐構成的幾何體,該正三棱錐的底面三角形內接于半球底面大圓,頂點在半球面上,則被挖去的正三棱錐體積為_______.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩位同學參加詩詞大賽,各答3道題,每人答對每道題的概率均為![]() ,且各人是否答對每道題互不影響.
,且各人是否答對每道題互不影響.
(Ⅰ)用![]() 表示甲同學答對題目的個數,求隨機變量
表示甲同學答對題目的個數,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(Ⅱ)設![]() 為事件“甲比乙答對題目數恰好多2”,求事件
為事件“甲比乙答對題目數恰好多2”,求事件![]() 發生的概率.
發生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為評估設備![]() 生產某種零件的性能,從設備
生產某種零件的性能,從設備![]() 生產零件的流水線上隨機抽取100件零件作為樣本,測量其直徑后,整理得到下表:
生產零件的流水線上隨機抽取100件零件作為樣本,測量其直徑后,整理得到下表:
直徑 | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合計 |
件數 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
經計算,樣本的平均值![]() ,標準差
,標準差![]() ,以頻率值作為概率的估計值.
,以頻率值作為概率的估計值.
(1)由以往統計數據知,設備的性能根據以下不等式進行評判(![]() 表示相應事件的概率);①
表示相應事件的概率);①![]() ;②
;②![]() ;③
;③![]() ,評判規則為:若同時滿足上述三個不等式,則設備等級為甲;僅滿足其中兩個,則等級為乙;若僅滿足其中一個,則等級為丙;若全部不滿足,則等級為丁.為評判一臺設備
,評判規則為:若同時滿足上述三個不等式,則設備等級為甲;僅滿足其中兩個,則等級為乙;若僅滿足其中一個,則等級為丙;若全部不滿足,則等級為丁.為評判一臺設備![]() 的性能,從該設備加工的零件中任意抽取一件,記其直徑為
的性能,從該設備加工的零件中任意抽取一件,記其直徑為![]() ,試判斷設備
,試判斷設備![]() 的性能等級
的性能等級
(2)將直徑小于等于![]() 或直徑大于
或直徑大于![]() 的零件認為是次品.
的零件認為是次品.
(i)若從設備![]() 的生產流水線上隨意抽取2件零件,求恰有一件次品的概率;
的生產流水線上隨意抽取2件零件,求恰有一件次品的概率;
(ii)若從樣本中隨意抽取2件零件,計算其中次品個數![]() 分布列和數學期望
分布列和數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com