【題目】如圖，直角
中，
，
，D，E分別是AB，BC邊的中點，沿DE將
折起至
，且
.
（1）求四棱錐
的體積；
（2）求證：平面
平面ACF.
陽光試卷單元測試卷系列答案科目：高中數學 來源： 題型：
【題目】已知集合
，集合
，
，
滿足.
①每個集合都恰有5個元素
② 
集合
中元素的最大值與最小值之和稱為集合的特征數，記為
，則
的值不可能為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某基地蔬菜大棚采用水培、無土栽培方式種植各類蔬菜．過去50周的資料顯示，該地周光照量
（小時）都在30小時以上，其中不足50小時的周數有5周，不低于50小時且不超過70小時的周數有35周，超過70小時的周數有10周．根據統計，該基地的西紅柿增加量
（百斤）與使用某種液體肥料
（千克）之間對應數據為如圖所示的折線圖．
（1）依據數據的折線圖，是否可用線性回歸模型擬合與的關系？請計算相關系數
并加以說明（精確到0．01）．（若
，則線性相關程度很高，可用線性回歸模型擬合）
（2）蔬菜大棚對光照要求較大，某光照控制儀商家為該基地提供了部分光照控制儀，但每周光照控制儀最多可運行臺數受周光照量限制，并有如下關系：
周光照量 |
|
|
|
光照控制儀最多可運行臺數 | 3 | 2 | 1 |
若某臺光照控制儀運行，則該臺光照控制儀周利潤為3000元；若某臺光照控制儀未運行，則該臺光照控制儀周虧損1000元．若商家安裝了3臺光照控制儀，求商家在過去50周周總利潤的平均值．
附：相關系數公式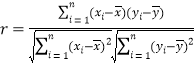
，參考數據
，
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我國古代名著《張丘建算經》中記載：“今有方錐，下廣二丈，高三丈.欲斬末為方亭，令上方六尺.問：斬高幾何？”大致意思是：有一個正四棱錐下底邊長為二丈，高三丈，現從上面截去一段，使之成為正四棱臺，且正四棱臺的上底邊長為六尺，則截去的正四棱錐的高是多少.如果我們把求截去的正四棱錐的高改為求剩下的正四棱臺的體積，則該正四棱臺的體積是（注：1丈
尺）（ ）
A.1946立方尺B.3892立方尺C.7784立方尺D.11676立方尺
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知某產品的歷史收益率的頻率分布直方圖如圖所示.
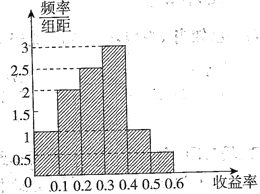
（1）試估計該產品收益率的中位數；
（2）若該產品的售價
（元）與銷量
（萬份）之間有較強線性相關關系，從歷史銷售記錄中抽樣得到如表5組
與
的對應數據：
售價 | 25 | 30 | 38 | 45 | 52 |
銷量 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
根據表中數據算出
關于
的線性回歸方程為
，求
的值；
（3）若從表中五組銷量數據中隨機抽取兩組，記其中銷量超過6萬份的組數為
，求
的分布列及期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，三棱柱
中，
側面
，已知
，
，
，點E是棱
的中點．
（1）求證：
平面ABC；
（2）在棱CA上是否存在一點M，使得EM與平面
所成角的正弦值為
，若存在，求出
的值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知動直線
：
與
軸交于點
，過點作直線
，交
軸于點
，點
滿足
，的軌跡為
.
（1）求的方程；
（2）已知點
，點
，過
作斜率為
的直線交于
，
兩點，延長
，
分別交于
，
兩點，記直線
的斜率為
，求證：
為定值.
查看答案和解析>>
科目：高中數學 來源： 題型：
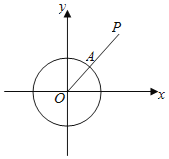
【題目】在平面直角坐標系xOy中，對于⊙O：x2+y2＝1來說，P是坐標系內任意一點，點P到⊙O的距離SP的定義如下：若P與O重合，SP＝r；若P不與O重合，射線OP與⊙O的交點為A，SP＝AP的長度（如圖）．
（1）直線2x+2y+1＝0在圓內部分的點到⊙O的最長距離為_____；
（2）若線段MN上存在點T，使得：
①點T在⊙O內；
②點P∈線段MN，都有ST≥SP成立．則線段MN的最大長度為_____．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
