
【題目】如圖,在四邊形![]() 中,
中,![]() ,
,![]() ,四邊形
,四邊形![]() 為矩形,且
為矩形,且![]() 平面
平面![]() ,
,![]() .
.
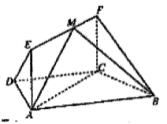
(1)求證:![]() 平面
平面![]() ;
;
(2)點![]() 在線段
在線段![]() 上運動,當點
上運動,當點![]() 在什么位置時,平面
在什么位置時,平面![]() 與平面
與平面![]() 所成銳二面角最大,并求此時二面角的余弦值.
所成銳二面角最大,并求此時二面角的余弦值.
【答案】(1)見解析;(2)![]()
【解析】試題分析:(Ⅰ)在梯形![]() 中,設
中,設![]() ,題意求得
,題意求得![]() ,再由余弦定理求得
,再由余弦定理求得![]() ,滿足
,滿足![]() ,得則
,得則![]() .再由
.再由![]() 平面
平面![]() 得
得![]() ,由線面垂直的判定可.進一步得到
,由線面垂直的判定可.進一步得到![]() 丄平面
丄平面![]() ;(Ⅱ)分別以直線
;(Ⅱ)分別以直線![]() 為:
為:![]() 軸,
軸,![]() 軸軸建立如圖所示的空間直角坐標系,設
軸軸建立如圖所示的空間直角坐標系,設![]() ,令
,令![]()
![]() 得到
得到![]() 的坐標,求出平面
的坐標,求出平面![]() 的一法向量.由題意可得平面的
的一法向量.由題意可得平面的![]() 一個法向量,求出兩法向量所成角的余弦值,可得當
一個法向量,求出兩法向量所成角的余弦值,可得當![]()
![]() 時,有最小值為
時,有最小值為![]() ,此時點
,此時點![]() 與點
與點![]() 重合.
重合.
試題解析:(Ⅰ)證明:在梯形![]() 中,∵
中,∵![]() ,設
,設![]() ,
,
又∵![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]() .則
.則![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,而
,而![]() ,∴
,∴![]() 平面
平面![]() .∵
.∵![]() ,∴
,∴![]() 平面
平面![]() .
.
(Ⅱ)解:分別以直線![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸建立如圖所示的空間直角坐標系,
軸建立如圖所示的空間直角坐標系,

設![]() ,令
,令![]() ,
,
則![]() ,
,
∴![]()
設![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
由 得
得![]() ,取
,取![]() ,則
,則![]() ,
,
∵![]() 是平面
是平面![]() 的一個法向量,
的一個法向量,
∴
∵![]() ,∴當
,∴當![]() 時,
時,![]() 有最小值為
有最小值為![]() ,
,
∴點![]() 與點
與點![]() 重合時,平面
重合時,平面![]() 與平面
與平面![]() 所成二面角最大,此時二面角的余弦值為
所成二面角最大,此時二面角的余弦值為![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=ex﹣ax﹣1,a∈R.
(1)當a=2時,求函數(shù)f(x)的單調(diào)性;
(2)設a≤0,求證:x≥0時,f(x)≥x2.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,點E為正方形ABCD邊CD上異于點C、D的動點,將△ADE沿AE翻折成△SAE,在翻折過程中,下列三個說法中正確的個數(shù)是( )
①存在點E和某一翻折位置使得AE∥平面SBC;
②存在點E和某一翻折位置使得SA⊥平面SBC;
③二面角S﹣AB﹣E的平面角總是小于2∠SAE.
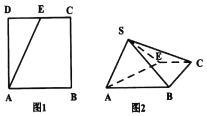
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】現(xiàn)定義:設![]() 是非零實常數(shù),若對于任意的
是非零實常數(shù),若對于任意的![]() ,都有
,都有![]() ,則稱函數(shù)
,則稱函數(shù)![]() 為“關(guān)于的
為“關(guān)于的![]() 偶型函數(shù)”
偶型函數(shù)”
(1)請以三角函數(shù)為例,寫出一個“關(guān)于2的偶型函數(shù)”的解析式,并給予證明
(2)設定義域為的“關(guān)于的![]() 偶型函數(shù)”在區(qū)間
偶型函數(shù)”在區(qū)間![]() 上單調(diào)遞增,求證在區(qū)間
上單調(diào)遞增,求證在區(qū)間![]() 上單調(diào)遞減
上單調(diào)遞減
(3)設定義域為![]() 的“關(guān)于
的“關(guān)于![]() 的偶型函數(shù)”
的偶型函數(shù)”![]() 是奇函數(shù),若
是奇函數(shù),若![]() ,請猜測
,請猜測![]() 的值,并用數(shù)學歸納法證明你的結(jié)論
的值,并用數(shù)學歸納法證明你的結(jié)論
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]() 中,
中,![]()
![]() ,又數(shù)列
,又數(shù)列![]() 滿足:
滿足:![]() .
.
(1)求證:數(shù)列![]() 是等比數(shù)列;
是等比數(shù)列;
(2)若數(shù)列![]() 是單調(diào)遞增數(shù)列,求實數(shù)
是單調(diào)遞增數(shù)列,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若數(shù)列![]() 的各項皆為正數(shù),
的各項皆為正數(shù),![]() ,設
,設![]() 是數(shù)列
是數(shù)列![]() 的前
的前![]() 項和,問:是否存在整數(shù)
項和,問:是否存在整數(shù)![]() ,使得數(shù)列
,使得數(shù)列![]() 是單調(diào)遞減數(shù)列?若存在,求出整數(shù)
是單調(diào)遞減數(shù)列?若存在,求出整數(shù)![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】至![]() 年底,我國發(fā)明專利申請量已經(jīng)連續(xù)
年底,我國發(fā)明專利申請量已經(jīng)連續(xù)![]() 年位居世界首位,下表是我國
年位居世界首位,下表是我國![]() 年至
年至![]() 年發(fā)明專利申請量以及相關(guān)數(shù)據(jù).
年發(fā)明專利申請量以及相關(guān)數(shù)據(jù).
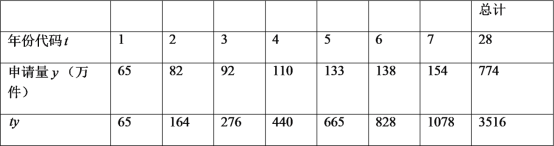
注:年份代碼![]() ~
~![]() 分別表示
分別表示![]() ~
~![]() .
.
(1)可以看出申請量每年都在增加,請問這幾年中哪一年的增長率達到最高,最高是多少?
(2)建立![]() 關(guān)于
關(guān)于![]() 的回歸直線方程(精確到
的回歸直線方程(精確到![]() ),并預測我國發(fā)明專利申請量突破
),并預測我國發(fā)明專利申請量突破![]() 萬件的年份.
萬件的年份.
參考公式:回歸直線的斜率和截距的最小二乘法估計分別為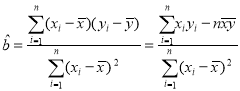 ,
,![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】謝爾賓斯基三角形(Sierpinski triangle)是一種分形幾何圖形,由波蘭數(shù)學家謝爾賓斯基在1915年提出,它是一個自相似的例子,其構(gòu)造方法是:
(1)取一個實心的等邊三角形(圖1);
(2)沿三邊中點的連線,將它分成四個小三角形;
(3)挖去中間的那一個小三角形(圖2);
(4)對其余三個小三角形重復(1)(2)(3)(4)(圖3).
制作出來的圖形如圖4,….
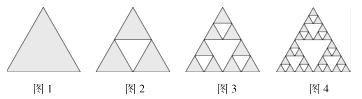
若圖1(陰影部分)的面積為1,則圖4(陰影部分)的面積為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】峰谷電是目前在城市居民當中開展的一種電價類別.它是將一天24小時劃分成兩個時間段,把8:00—22:00共14小時稱為峰段,執(zhí)行峰電價,即電價上調(diào);22:00—次日8:00共10個小時稱為谷段,執(zhí)行谷電價,即電價下調(diào).為了進一步了解民眾對峰谷電價的使用情況,從某市一小區(qū)隨機抽取了50 戶住戶進行夏季用電情況調(diào)查,各戶月平均用電量以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (單位:度)分組的頻率分布直方圖如下圖:
(單位:度)分組的頻率分布直方圖如下圖:

若將小區(qū)月平均用電量不低于700度的住戶稱為“大用戶”,月平均用電量低于700度的住戶稱為“一般用戶”.其中,使用峰谷電價的戶數(shù)如下表:
月平均用電量(度) |
|
|
|
|
|
|
使用峰谷電價的戶數(shù) | 3 | 9 | 13 | 7 | 2 | 1 |
(1)估計所抽取的 50戶的月均用電量的眾數(shù)和平均數(shù)(同一組中的數(shù)據(jù)用該組區(qū)間的中點值作代表);
(2)(![]() )將“一般用戶”和“大用戶”的戶數(shù)填入下面
)將“一般用戶”和“大用戶”的戶數(shù)填入下面![]() 的列聯(lián)表:
的列聯(lián)表:
一般用戶 | 大用戶 | |
使用峰谷電價的用戶 | ||
不使用峰谷電價的用戶 |
(![]() )根據(jù)(
)根據(jù)(![]() )中的列聯(lián)表,能否有
)中的列聯(lián)表,能否有![]() 的把握認為 “用電量的高低”與“使用峰谷電價”有關(guān)?
的把握認為 “用電量的高低”與“使用峰谷電價”有關(guān)?
| 0.025 | 0.010 | 0.001 |
| 5.024 | 6.635 | 10.828 |
附:![]() ,
,
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com