
【題目】某水產(chǎn)品經(jīng)銷商銷售某種鮮魚,售價為每公斤![]() 元,成本為每公斤
元,成本為每公斤![]() 元.銷售宗旨是當天進貨當天銷售.如果當天賣不出去,未售出的全部降價處理完,平均每公斤損失
元.銷售宗旨是當天進貨當天銷售.如果當天賣不出去,未售出的全部降價處理完,平均每公斤損失![]() 元.根據(jù)以往的銷售情況,按
元.根據(jù)以往的銷售情況,按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 進行分組,得到如圖所示的頻率分布直方圖.
進行分組,得到如圖所示的頻率分布直方圖.
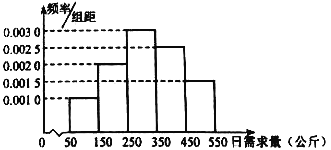
(1)求未來連續(xù)三天內(nèi),該經(jīng)銷商有連續(xù)兩天該種鮮魚的日銷售量不低于![]() 公斤,而另一天日銷售量低于
公斤,而另一天日銷售量低于![]() 公斤的概率;
公斤的概率;
(2)在頻率分布直方圖的需求量分組中,以各組區(qū)間的中點值代表該組的各個值.
(i)求日需求量![]() 的分布列;
的分布列;
(ii)該經(jīng)銷商計劃每日進貨![]() 公斤或
公斤或![]() 公斤,以每日利潤
公斤,以每日利潤![]() 的數(shù)學期望值為決策依據(jù),他應(yīng)該選擇每日進貨
的數(shù)學期望值為決策依據(jù),他應(yīng)該選擇每日進貨![]() 公斤還是
公斤還是![]() 公斤?
公斤?
【答案】(1)0.192(2) (ⅰ)見解析(ⅱ)該經(jīng)銷商應(yīng)該選擇每日進貨400公斤
【解析】試題分析:(1)根據(jù)頻率分布直方圖得到不低于350公斤的概率為0.4,有連續(xù)兩天該種鮮魚的日銷售量不低于![]() 公斤,而另一天日銷售量低于
公斤,而另一天日銷售量低于![]() 公斤的概率即分兩種情況按照概率相乘計算即可;(2)(i)X可取100,200,300,400,500,根據(jù)圖得到對應(yīng)的長方形的概率值,(ii)根據(jù)題意求出進貨量為300,400時的利潤均值,選擇較高的即可.
公斤的概率即分兩種情況按照概率相乘計算即可;(2)(i)X可取100,200,300,400,500,根據(jù)圖得到對應(yīng)的長方形的概率值,(ii)根據(jù)題意求出進貨量為300,400時的利潤均值,選擇較高的即可.
解析;’
(Ⅰ)由頻率分布直方圖可知,
日銷售量不低于350公斤的概率為(0.0025+0.0015)×100=0.4,
則未來連續(xù)三天內(nèi),有連續(xù)兩天的日銷售量不低于350公斤,而另一天日銷售量低于350公斤的概率P=0.4×0.4×(1-0.4)+(1-0.4)×0.4×0.4=0.192.
(Ⅱ)(ⅰ)X可取100,200,300,400,500,
P(X=100)=0.0010×10=0.1; P(X=200)=0.0020×10=0.2;
P(X=300)=0.0030×10=0.3; P(X=400)=0.0025×10=0.25;
P(X=500)=0.0015×10=0.15;
所以X的分布列為:

(ⅱ)當每日進貨300公斤時,利潤Y1可取-100,700,1500,
此時Y1的分布列為:
![]()
此時利潤的期望值E(Y1)=-100×0.1+700×0.2+1500×0.7=1180;
當每日進貨400公斤時,利潤Y2可取-400,400,1200,2000,
此時Y2的分布列為:

此時利潤的期望值E(Y2)=-400×0.1+400×0.2+1200×0.3+2000×0.4=1200;
因為E(Y1)<E(Y2),
所以該經(jīng)銷商應(yīng)該選擇每日進貨400公斤.


 倍速訓練法直通中考考點系列答案
倍速訓練法直通中考考點系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作業(yè)本系列答案
名校作業(yè)本系列答案 輕巧奪冠周測月考直通名校系列答案
輕巧奪冠周測月考直通名校系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且經(jīng)過點
,且經(jīng)過點![]() .
.
(1)求橢圓的標準方程;
(2)過點![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() 兩點,
兩點,![]() 是
是![]() 軸上的點,若
軸上的點,若![]() 是以
是以![]() 為斜邊的等腰直角三角形, 求直線
為斜邊的等腰直角三角形, 求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】2017年8月20日起,市交警支隊全面啟動路口秩序環(huán)境綜合治理,重點整治機動車不禮讓斑馬線和行人的行為,經(jīng)過一段時間的治理,從市交警隊數(shù)據(jù)庫中調(diào)取了20個路口近三個月的車輛違章數(shù)據(jù),經(jīng)統(tǒng)計得如圖所示的頻率分布直方圖,統(tǒng)計數(shù)據(jù)中凡違章車次超過30次的設(shè)為“重點關(guān)注路口”.
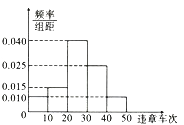
(1)現(xiàn)從“重點關(guān)注路口”中隨機抽取兩個路口安排交警去執(zhí)勤,求抽出來的路口的違章車次一個在![]() ,一個在
,一個在![]() 中的概率;
中的概率;
(2)現(xiàn)從支隊派遣5位交警,每人選擇一個路口執(zhí)勤,每個路口至多1人,違章車次在![]() 的路口必須有交警去,違章車次在
的路口必須有交警去,違章車次在![]() 的不需要交警過去,設(shè)去“重點關(guān)注路口”的交警人數(shù)為
的不需要交警過去,設(shè)去“重點關(guān)注路口”的交警人數(shù)為![]() ,求
,求![]() 的分布列及數(shù)學期望.
的分布列及數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】四棱錐![]() 中,
中,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,BC//AD,已知Q是四邊形ABCD內(nèi)部一點,且二面角
,BC//AD,已知Q是四邊形ABCD內(nèi)部一點,且二面角![]() 的平面角大小為
的平面角大小為![]() ,若動點Q的軌跡將ABCD分成面積為
,若動點Q的軌跡將ABCD分成面積為![]() 的兩部分,則
的兩部分,則![]() =_______.
=_______.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某產(chǎn)品按行業(yè)生產(chǎn)標準分成8個等級,等級系數(shù)X依次為1,2,…8,其中![]() 為標準,
為標準,![]() 為標準. 已知甲廠執(zhí)行標準生產(chǎn)該產(chǎn)品,產(chǎn)品的零售價為6元/件; 乙廠執(zhí)行標準生產(chǎn)該產(chǎn)品,產(chǎn)品的零售價為元/件,假定甲, 乙兩廠的產(chǎn)品都符合相應(yīng)的執(zhí)行標準.
為標準. 已知甲廠執(zhí)行標準生產(chǎn)該產(chǎn)品,產(chǎn)品的零售價為6元/件; 乙廠執(zhí)行標準生產(chǎn)該產(chǎn)品,產(chǎn)品的零售價為元/件,假定甲, 乙兩廠的產(chǎn)品都符合相應(yīng)的執(zhí)行標準.
(Ⅰ)已知甲廠產(chǎn)品的等級系數(shù)![]() 的概率分布列如下所示:
的概率分布列如下所示:
| 5 | 6 | 7 | 8 |
0.4 | b | 0.1 |
且![]() 的數(shù)學期望
的數(shù)學期望![]() , 求a,b的值;
, 求a,b的值;
(Ⅱ)為分析乙廠產(chǎn)品的等級系數(shù)![]() ,從該廠生產(chǎn)的產(chǎn)品中隨機抽取30件,相應(yīng)的等級系數(shù)組成一個樣本,數(shù)據(jù)如下:
,從該廠生產(chǎn)的產(chǎn)品中隨機抽取30件,相應(yīng)的等級系數(shù)組成一個樣本,數(shù)據(jù)如下:

用這個樣本的頻率分布估計總體分布,將頻率視為概率,求等級系數(shù)![]() 的數(shù)學期望;
的數(shù)學期望;
(Ⅲ)在(Ⅰ),(Ⅱ)的條件下,若以“性價比”為判斷標準,則哪個工廠的產(chǎn)品更具可購買性?說明理由.
注: ①產(chǎn)品的“性價比”=![]() ;②“性價比”大的產(chǎn)品更具可購買性.
;②“性價比”大的產(chǎn)品更具可購買性.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
已知曲線![]() 在平面直角坐標系
在平面直角坐標系![]() 下的參數(shù)方程為
下的參數(shù)方程為 (
(![]() 為參數(shù)),以坐標原點
為參數(shù)),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系.
軸正半軸為極軸,建立極坐標系.
(1)求曲線![]() 的普通方程及極坐標方程;
的普通方程及極坐標方程;
(2)直線![]() 的極坐標方程是
的極坐標方程是![]() ,射線
,射線![]() :
: ![]() 與曲線
與曲線![]() 交于點
交于點![]() 與直線
與直線![]() 交于點
交于點![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com