
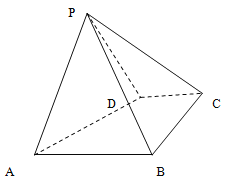
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,側面
,側面![]() 底面
底面![]() ,且
,且![]() 是以
是以![]() 為底的等腰三角形.
為底的等腰三角形.
(Ⅰ)證明:![]()
(Ⅱ)若四棱錐![]() 的體積等于
的體積等于![]() .問:是否存在過點
.問:是否存在過點![]() 的平面
的平面![]() 分別交
分別交![]() ,
,![]() 于點
于點![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的面積;若不存在,請說明理由.
的面積;若不存在,請說明理由.
【答案】(Ⅰ)見解析;(Ⅱ)![]() .
.
【解析】試題分析: (Ⅰ)取![]() 的中
的中![]() ,連接
,連接![]() ,由三角形
,由三角形![]() 是等腰三角形,則
是等腰三角形,則![]() ,又
,又![]() ,可得
,可得![]() ,從而證出
,從而證出![]() ,可得
,可得![]() ; (Ⅱ)取
; (Ⅱ)取![]() 中點
中點![]() ,連接
,連接![]() ,可證明四邊形
,可證明四邊形![]() 為平行四邊形,進一步證明
為平行四邊形,進一步證明![]() ,可得三角形
,可得三角形![]() 是直角三角形,由三角形面積公式可得面積.
是直角三角形,由三角形面積公式可得面積.
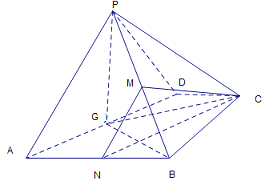
試題解析:(Ⅰ)證明:取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,
∵![]() ,
,
∴![]() .
.
∵![]() 且
且![]() ,
,
∴![]() 是正三角形,且
是正三角形,且![]() ,
,
又∵![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() ,且
,且![]() 平面
平面![]()
∴![]()
(Ⅱ)解:存在,理由如下:
分別取![]() 的中點
的中點![]() ,連接
,連接![]() ,則
,則![]() ;
;
∵![]() 是梯形,
是梯形,![]() 且
且![]() ,
,
∴![]() 且
且![]() ,則四邊形
,則四邊形![]() 為平行四邊形,
為平行四邊形,
∴![]()
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() 平面
平面![]() ,
,![]() 平面
平面![]() 且
且![]() 平面
平面![]() ,
,![]()
∴平面![]() 平面
平面![]()
∵側面![]() ,且平面
,且平面![]() 平面
平面![]()
由(Ⅰ)知,![]() 平面
平面![]() ,若四棱錐
,若四棱錐![]() 的體積等于
的體積等于![]() ,
,
則![]() ,所以
,所以![]()
在![]() 和
和![]() 中,
中,![]()
∴![]() ,則
,則![]()
∴![]() 是直角三角形,則
是直角三角形,則![]() .
.


科目:高中數學 來源: 題型:
【題目】【選修4-4:坐標系與參數方程】
在直角坐標系![]() 中,以原點
中,以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),曲線
為參數),曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若點![]() 的坐標為
的坐標為![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,原點為
,原點為![]() ,橢圓
,橢圓![]() 的動弦
的動弦![]() 過焦點
過焦點![]() 且不垂直于坐標軸,弦
且不垂直于坐標軸,弦![]() 的中點為
的中點為![]() ,過
,過![]() 且垂直于線段
且垂直于線段![]() 的直線交射線
的直線交射線![]() 于點
于點![]() .
.
(1)證明:點![]() 在定直線上;
在定直線上;
(2)當![]() 最大時,求
最大時,求![]() 的面積.
的面積.

查看答案和解析>>
科目:高中數學 來源: 題型:
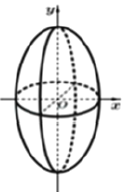
【題目】祖暅是我國齊梁時代的數學家,是祖沖之的兒子,他提出了一條原理:“冪勢既同,則積不容易.”這里的“冪”指水平截面的面積.“勢”指高,這句話的意思是:兩個等高的幾何體若在所有等高處的水平截面的面積相等,則這兩個幾何體體積相等。于是可把半徑相等的半球(底面在下)和圓柱(圓柱高等于半徑)放在同一水平面上,圓柱里再放一個半徑和高都與圓柱相等的圓錐(錐尖朝下),考察圓柱里被圓錐截剩的立體,這樣在同一高度用平行平面截得的半球截面和圓柱中剩余立體截得的截面面積相等,因此半球的體積等于圓柱中剩余立體的體積.設由橢圓![]() 所圍成的平面圖形繞
所圍成的平面圖形繞![]() 軸旋轉一周后,得一橄欖狀的幾何體(如圖,稱為“橢球體”),請類比以上所介紹的應用祖暅原理求球體體積的做法求這個橢球體的體積.其體積等于________.
軸旋轉一周后,得一橄欖狀的幾何體(如圖,稱為“橢球體”),請類比以上所介紹的應用祖暅原理求球體體積的做法求這個橢球體的體積.其體積等于________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某老師對全班![]() 名學生學習積極性和參加社團活動情況進行調查,統計數據如下所示:
名學生學習積極性和參加社團活動情況進行調查,統計數據如下所示:
參加社團活動 | 不參加社團活動 | 合計 | |
學習積極性高 |
| ||
學習積極性一般 |
| ||
合計 |
|
|
(1)請把表格數據補充完整;
(2)若從不參加社團活動的![]() 人按照分層抽樣的方法選取
人按照分層抽樣的方法選取![]() 人,再從所選出的
人,再從所選出的![]() 人中隨機選取兩人作為代表發言,求至少有一個學習積極性高的概率;
人中隨機選取兩人作為代表發言,求至少有一個學習積極性高的概率;
(3)運用獨立性檢驗的思想方法分析:請你判斷是否有![]() 的把握認為學生的學習積極性與參與社團活動由關系?
的把握認為學生的學習積極性與參與社團活動由關系?
附: 
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為評估設備![]() 生產某種零件的性能,從設備
生產某種零件的性能,從設備![]() 生產零件的流水線上隨機抽取100件零件作為樣本,測量其直徑后,整理得到下表:
生產零件的流水線上隨機抽取100件零件作為樣本,測量其直徑后,整理得到下表:
直徑/ | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合計 |
件數 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
經計算,樣本的平均值![]() ,標準差
,標準差![]() ,以頻率值作為概率的估計值.
,以頻率值作為概率的估計值.
(1)為評判一臺設備的性能,從該設備加工的零件中任意抽取一件,記其直徑為![]() ,并根據以下不等式進行評判(
,并根據以下不等式進行評判(![]() 表示相應事件的概率);
表示相應事件的概率);
①![]() ;
;
②![]() ;
;
③![]()
評判規則為:若同時滿足上述三個不等式,則設備等級為甲;僅滿足其中兩個,則等級為乙;若僅滿足其中一個,則等級為丙;若全部不滿足,則等級為丁,試判斷設備![]() 的性能等級.
的性能等級.
(2)將直徑小于等于![]() 或直徑大于
或直徑大于![]() 的零件認為是次品.
的零件認為是次品.
①從設備![]() 的生產流水線上隨意抽取2件零件,計算其中次品個數
的生產流水線上隨意抽取2件零件,計算其中次品個數![]() 的數學期望
的數學期望![]() ;
;
②從樣本中隨意抽取2件零件,計算其中次品個數![]() 的數學期望
的數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com