
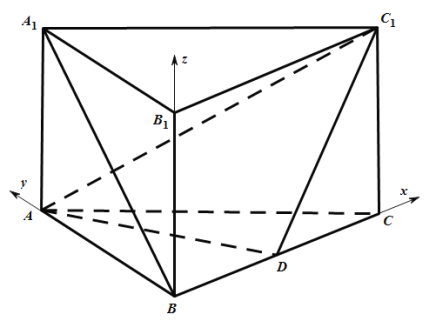
【題目】如圖,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中點.
的中點.
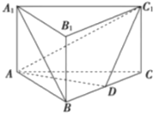
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)試問線段![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 與面
與面![]() 所成角的正弦值為
所成角的正弦值為![]() ?若存在,求出此時
?若存在,求出此時![]() 的長,若不存在,請說明理由.
的長,若不存在,請說明理由.
【答案】(1)證明見解析;(2)![]() ;(3)不存在,理由見解析
;(3)不存在,理由見解析
【解析】
(1)連接![]() 交
交![]() 于點
于點![]() ,得
,得![]() 是
是![]() 的中位線,再由線面平行的判定定理即可證明;
的中位線,再由線面平行的判定定理即可證明;
(2)建立直角坐標系,由兩個平面的法向量的夾角即可得出二面角;
(3)設點![]() ,
,![]() ,表示出向量
,表示出向量![]() ,由線面角的夾角公式求出
,由線面角的夾角公式求出![]() 的值即可判斷.
的值即可判斷.
(1)如圖,連接![]() 交
交![]() 于點
于點![]() ,
,
因為![]() 是直三棱柱,所以四邊形
是直三棱柱,所以四邊形![]() 是矩形,
是矩形,
點![]() 為
為![]() 的中點,又
的中點,又![]() 為
為![]() 中點,
中點,
所以![]() 是
是![]() 的中位線,所以
的中位線,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
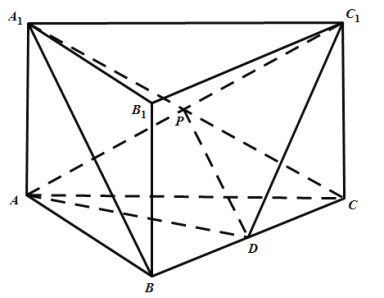
(2)因為![]() 是直三棱柱,
是直三棱柱,![]() ,所以
,所以![]() 、
、![]() 、
、![]() 兩兩垂直,
兩兩垂直,
如圖建立空間直角坐標系![]() ,設
,設![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
設平面![]() 的法向量
的法向量![]() ,則
,則
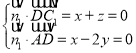 ,令
,令![]() ,則
,則![]() ,
,![]() ,
,
所以![]() ,
,
易知平面![]() 的法向量
的法向量![]() ,
,
由二面角![]() 是銳角,
是銳角,
所以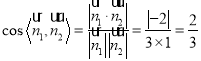 ,
,
即二面角![]() 的余弦值為
的余弦值為![]() ;
;
(3)設線段![]() 上存在點
上存在點![]() ,
,![]() ,
,
則![]() ,
,
由(2)知,平面平面![]() 的法向量
的法向量![]() ,
,
因為![]() 與面
與面![]() 所成角的正弦值為
所成角的正弦值為![]() ,
,
所以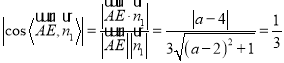 ,
,
解得![]() ,
,
所以在線段![]() 上不存在點
上不存在點![]() ,使得
,使得![]() 與面
與面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知圓![]() ,點
,點![]() ,點
,點![]() 在圓
在圓![]() 上運動,
上運動,![]() 的垂直平分線交
的垂直平分線交![]() 于點
于點![]() .
.
(1)求證:![]() 為定值及動點
為定值及動點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)不在![]() 軸上的
軸上的![]() 點為
點為![]() 上任意一點,
上任意一點,![]() 與
與![]() 關于原點
關于原點![]() 對稱,直線
對稱,直線![]() 交
交![]() 于另外一點
于另外一點![]() .求證:直線
.求證:直線![]() 與直線
與直線![]() 的斜率的乘積為定值,并求出該定值.
的斜率的乘積為定值,并求出該定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】世界讀書日又稱“世界圖書日”,設立的目的是希望世界各地的人,無論你是年老還是年輕,都能享受閱讀的樂趣,都能尊重和感謝為人類文明做出巨大貢獻的文學、文化、科學、思想大師們,都能保護知識產權.某單位共有600人,其年齡與人數分布表如下:
年齡段 |
|
|
|
|
人數(單位:人) | 150 | 210 | 180 | 60 |
約定:年齡在![]() 為青年人,在
為青年人,在![]() 為中老年人.今年年初,該單位開展“每天閱讀1小時”活動,為了了解員工閱讀1小時是否與年齡相關,一個月后按照分層抽樣抽取30人進行調查.
為中老年人.今年年初,該單位開展“每天閱讀1小時”活動,為了了解員工閱讀1小時是否與年齡相關,一個月后按照分層抽樣抽取30人進行調查.
(1)抽出的青年人與中老年人數量分別為多少?并估算單位這600人的平均年齡;
(2)若所抽取出的青年人與中老年人中分別有6人和7人平均每天閱讀達1小時,其余人都沒達1小時.完成下列2×2列聯表,并回答能否由90%的把握認為年齡與閱讀達1小時有關?
閱讀達1小時 | 閱讀沒達1小時 | 總計 | |
青年 | 6 | ||
中年 | 7 | ||
總計 | 30 |
參考公式: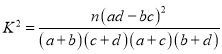
臨界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三棱錐P-ABC(如圖一)的平面展開圖(如圖二)中,四邊形ABCD為邊長等于![]() 的正方形,
的正方形,![]() 和
和![]() 均為正三角形,在三棱錐P-ABC中:
均為正三角形,在三棱錐P-ABC中:
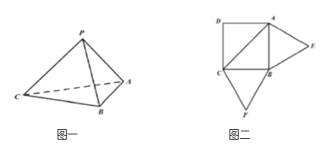
(1)證明:平面![]() 平面ABC;
平面ABC;
(2)若點M在棱PA上運動,當直線BM與平面PAC所成的角最大時,求直線MA與平面MBC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“紋樣”是中國藝術寶庫的瑰寶,“火紋”是常見的一種傳統紋樣,為了測算某火紋紋樣(如圖陰影部分所示)的面積,作一個邊長為3的正方形將其包含在內,并向該正方形內隨機投擲2000個點,己知恰有800個點落在陰影部分,據此可估計陰影部分的面積是

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AB//CD,且![]() .
.

(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:若函數![]() 的導函數
的導函數![]() 是奇函數(
是奇函數(![]() ),則稱函數
),則稱函數![]() 是“雙奇函數” .函數
是“雙奇函數” .函數![]() .
.
(1)若函數![]() 是“雙奇函數”,求實數
是“雙奇函數”,求實數![]() 的值;
的值;
(2)假設![]() .
.
(i)在(1)的條件下,討論函數![]() 的單調性;
的單調性;
(ii)若![]() ,討論函數
,討論函數![]() 的極值點.
的極值點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的參數方程為
的參數方程為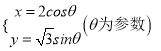 ,在同一平面直角坐標系中,將曲線
,在同一平面直角坐標系中,將曲線![]() 上的點按坐標變換
上的點按坐標變換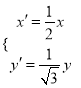 得到曲線
得到曲線![]() ,以原點為極點,
,以原點為極點, ![]() 軸的正半軸為極軸,建立極坐標系.
軸的正半軸為極軸,建立極坐標系.
(Ⅰ)求曲線![]() 的極坐標方程;
的極坐標方程;
(Ⅱ)若過點![]() (極坐標)且傾斜角為
(極坐標)且傾斜角為![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,弦
兩點,弦![]() 的中點為
的中點為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com