【題目】港珠澳大橋是中國建設史上里程最長，投資最多，難度最大的跨海橋梁項目，大橋建設需要許多橋梁構件。從某企業生產的橋梁構件中抽取
件，測量這些橋梁構件的質量指標值，由測量結果得到如圖所示的頻率分布直方圖，質量指標值落在區間
，
，
內的頻率之比為
.
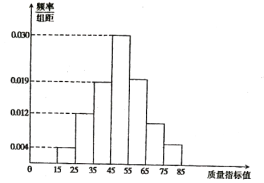
（1）求這些橋梁構件質量指標值落在區間內的頻率；
（2）用分層抽樣的方法在區間
內抽取一個容量為
的樣本，將該樣本看成一個總體，從中任意抽取
件橋梁構件，求這件橋梁構件都在區間
內的概率
【答案】(1)0.05(2) 
【解析】
（1）根據頻率分布直方圖中表示的頻率之和為1得到參數值；（2）先根據分層抽樣的原則得到每個區間內的樣本件數，再根據古典概型的計算公式列式得到結果即可.
（1）設這些橋梁構件質量指標值落在區間
內的頻率為
，則這些橋梁構件質量指標值落在區間
，
內的頻率分別為
和
.
依題意得
，解得
.
所以這些橋梁構件質量指標值落在區間內的頻率為
.
（2）由（I）得，這些橋梁構件質量指標值落在區間
，
，
內的頻率依次為
，
，
.
用分層抽樣的方法在區間
內抽取一個容量為
的樣本，則在區間
內應抽取
件，記為
，
，
.
在區間內應抽取
件，記為
，
在區間內應抽取
件，記為
.
設“從樣本中任意抽取
件產品，這件橋梁構件都在區間內”為事件
，則所有的基本事件有：
，
，
，
，
，
，
，
，
，
，
，
，
，
，共15種.
事件包含的基本事件有：
，
，，，
，，，，，共10種.
所以這件橋梁構件都在區間
內的概率為
.
春雨教育同步作文系列答案科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，平面
平面
，
，
，
，且
.
（1）過
作截面與線段
交于點H，使得
平面
，試確定點H的位置，并給出證明；
（2）在（1）的條件下，若二面角
的大小為
，試求直線
與平面所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
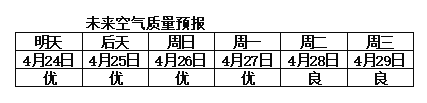
【題目】假設今天是4月23日，某市未來六天的空氣質量預報情況如下圖所示.該市有甲、乙、丙三人計劃在未來六天（4月24日～4月29日）內選擇一天出游，甲只選擇空氣質量為優的一天出游，乙不選擇周一出游，丙不選擇明天出游，且甲與乙不選擇同一天出游，則這三人出游的不同方法數為________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】橢圓
，
是橢圓
的左右頂點，點P是橢圓上的任意一點.
（1）證明：直線
，與直線
，斜率之積為定值.
（2）設經過
且斜率不為0的直線
交橢圓于
兩點，直線
與直線
交于點
，求證：
為定值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[選修4-4：坐標系與參數方程]
已知曲線
的極坐標方程為
，以極點
為直角坐標原點，以極軸為
軸的正半軸建立平面直角坐標系
，將曲線向左平移
個單位長度，再將得到的曲線上的每一個點的橫坐標縮短為原來的
，縱坐標保持不變，得到曲線
（1）求曲線的直角坐標方程；
（2）已知直線
的參數方程為
，（
為參數），點
為曲線上的動點，求點到直線距離的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司準備上市一款新型轎車零配件，上市之前擬在其一個下屬4S店進行連續30天的試銷.定價為1000元/件.試銷結束后統計得到該4S店這30天內的日銷售量（單位：件）的數據如下表：
日銷售量 | 40 | 60 | 80 | 100 |
頻數 | 9 | 12 | 6 | 3 |
（1）若該4S店試銷期間每個零件的進價為650元/件，求試銷連續30天中該零件日銷售總利潤不低于24500元的頻率；
（2）試銷結束后，這款零件正式上市，每個定價仍為1000元，但生產公司對該款零件不零售，只提供零件的整箱批發，大箱每箱有60件，批發價為550元/件；小箱每箱有45件，批發價為600元/件.該4S店決定每天批發兩箱，根據公司規定，當天沒銷售出的零件按批發價的9折轉給該公司的另一下屬4S店.假設該4店試銷后的連續30天的日銷售量（單位：件）的數據如下表：
日銷售量 | 50 | 70 | 90 | 110 |
頻數 | 5 | 15 | 8 | 2 |
（ⅰ）設該4S店試銷結束后連續30天每天批發兩大箱，這30天這款零件的總利潤；
（ⅱ）以總利潤作為決策依據，該4S店試銷結束后連續30天每天應該批發兩大箱還是兩小箱？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2020年寒假是特殊的寒假，因為抗擊疫情全體學生只能在家進行網上在線學習，為了研究學生在網上學習的情況，某學校在網上隨機抽取120名學生對線上教育進行調查，其中男生與女生的人數之比為11∶13，其中男生30人對于線上教育滿意，女生中有15名表示對線上教育不滿意.
（1）完成
列聯表，并回答能否有99%的把握認為對“線上教育是否滿意與性別有關”；
滿意 | 不滿意 | 總計 | |
男生 | 30 | ||
女生 | 15 | ||
合計 | 120 |
（2）從被調查的對線上教育滿意的學生中，利用分層抽樣抽取8名學生，再在8名學生中抽取3名學生，作線上學習的經驗介紹，其中抽取男生的個數為
，求出的分布列及期望值.
參考公式：附：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 0.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】針對時下的“抖音熱”，某校團委對“學生性別和喜歡抖音是否有關”作了一次調查，其中被調查的男女生人數相同，男生喜歡抖音的人數占男生人數的
，女生喜歡抖音的人數占女生人數
，若有95%的把握認為是否喜歡抖音和性別有關則調查人數中男生可能有（ ）人
附表：
| 0.050 | 0.010 |
k | 3.841 | 6.635 |
附：
A.25或45B.45C.45或60D.75或60
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
