
【題目】如圖,PDCE為矩形,ABCD為梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=![]() CD=1,PD=
CD=1,PD=![]() .
.

(1)若M為PA中點,求證:AC∥平面MDE;
(2)求直線PE與平面PBC所成角的正弦值.
(3)在PC上是否存在一點Q,使得平面QAD與平面PBC所成銳二面角的大小為![]() .
.
【答案】(1)證明見解析(2)![]() (3)存在
(3)存在
【解析】
(1)連結PC,交DE與N,可得N為PC中點,結合已知,可證MN∥AC,即可證明結論;
(2)建立空間直角坐標系,求出![]() 坐標,進而求出
坐標,進而求出![]() 坐標及平面PBC法向量坐標,根據空間向量的線面角公式,即可求解;
坐標及平面PBC法向量坐標,根據空間向量的線面角公式,即可求解;
(3)設![]() ,求出平面
,求出平面![]() 的法向量坐標,按照空間向量的面面角公式,求出
的法向量坐標,按照空間向量的面面角公式,求出![]() ,并判斷是否滿足條件.
,并判斷是否滿足條件.
(1)連結PC,交DE與N,連結MN,
∵△PAC中,M,N分別為兩腰PA,PC的中點,
∴MN∥AC因為MN面MDE,又![]() 面MDE,
面MDE,
所以AC∥平面MDE
(2)∵∠ADC=90°,∴AD⊥DC,又AD平面ABCD,
平面PDCE∩平面ABCD![]() ,∴AD⊥平面PDCE,
,∴AD⊥平面PDCE,
又PD平面PDCE,∴AD⊥PD,以D為空間坐標系的原點,
分別以DA,DC,DP所在直線為x,y,z軸建立空間直角坐標系,
則![]() ,
,![]() ,
,
![]() ,設面PBC的法向量
,設面PBC的法向量![]() ,應有
,應有 即:
即:
令![]() ,則
,則![]() ,所以
,所以![]() ,
,
設PE與PBC所成角的大小為θ,∵![]() ,
,
∴![]() ,
,
直線PE與平面PBC所成角的正弦值![]() .
.
(3)設![]() 則
則
![]()
![]() ,設平面QAD的法向量為
,設平面QAD的法向量為![]() ,
,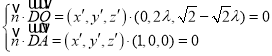 即:
即:
則![]() ,令
,令![]() ,則
,則![]() ,所以
,所以![]()
∵面PBC的法向量![]() ,
,
平面QAD與平面PBC所成銳二面角的大小為![]() .∴
.∴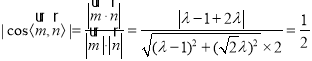 ,
,
整理得![]() ,解得
,解得![]() 或
或![]() ,
,
∴PC上存在點Q滿足條件,Q與P重合,或![]() .
.



 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:高中數學 來源: 題型:
【題目】已知雙曲線過點(3,-2)且與橢圓4x2+9y2=36有相同的焦點.
(1)求雙曲線的標準方程;
(2)若點M在雙曲線上,F1,F2為左、右焦點,且|MF1|+|MF2|=6![]() ,試判別△MF1F2的形狀.
,試判別△MF1F2的形狀.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在長方體ABCD﹣A1B1C1D1,若AB=BC,E,F分別是AB1,BC1的中點,則下列結論中不成立的是( )
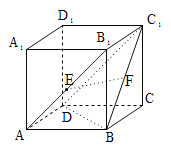
A.EF與BB1垂直B.EF⊥平面BDD1B1
C.EF與C1D所成的角為45°D.EF∥平面A1B1C1D1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】AB是圓O的直徑,點C是圓O上異于AB的動點,過動點C的直線VC垂直于圓O所在平面,D,E分別是VA,VC的中點.
(1)判斷直線DE與平面VBC的位置關系,并說明理由;
(2)當△VAB為邊長為![]() 的正三角形時,求四面體V﹣DEB的體積.
的正三角形時,求四面體V﹣DEB的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
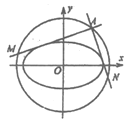
【題目】已知![]() 是圓
是圓![]() 上的一個動點,過點
上的一個動點,過點![]() 作兩條直線
作兩條直線![]() ,它們與橢圓
,它們與橢圓![]() 都只有一個公共點,且分別交圓于點
都只有一個公共點,且分別交圓于點![]() .
.
(Ⅰ)若![]() ,求直線
,求直線![]() 的方程;
的方程;
(Ⅱ)①求證:對于圓上的任意點![]() ,都有
,都有![]() 成立;
成立;
②求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】AB是圓O的直徑,點C是圓O上異于AB的動點,過動點C的直線VC垂直于圓O所在平面,D,E分別是VA,VC的中點.
(1)判斷直線DE與平面VBC的位置關系,并說明理由;
(2)當△VAB為邊長為![]() 的正三角形時,求四面體V﹣DEB的體積.
的正三角形時,求四面體V﹣DEB的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某書店剛剛上市了《中國古代數學史》,銷售前該書店擬定了5種單價進行試銷,每種單價(![]() 元)試銷l天,得到如表單價
元)試銷l天,得到如表單價![]() (元)與銷量
(元)與銷量![]() (冊)數據:
(冊)數據:
單價 | 18 | 19 | 20 | 21 | 22 |
銷量 | 61 | 56 | 50 | 48 | 45 |
(l)根據表中數據,請建立![]() 關于
關于![]() 的回歸直線方程:
的回歸直線方程:
(2)預計今后的銷售中,銷量![]() (冊)與單價
(冊)與單價![]() (元)服從(l)中的回歸方程,已知每冊書的成本是12元,書店為了獲得最大利潤,該冊書的單價應定為多少元?
(元)服從(l)中的回歸方程,已知每冊書的成本是12元,書店為了獲得最大利潤,該冊書的單價應定為多少元?
附: ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】空氣質量指數![]() 是檢測空氣質量的重要參數,其數值越大說明空氣污染狀況越嚴重,空氣質量越差.某地環保部門統計了該地區某月1日至24日連續24天的空氣質量指數
是檢測空氣質量的重要參數,其數值越大說明空氣污染狀況越嚴重,空氣質量越差.某地環保部門統計了該地區某月1日至24日連續24天的空氣質量指數![]() ,根據得到的數據繪制出如圖所示的折線圖,則下列說法錯誤的是( )
,根據得到的數據繪制出如圖所示的折線圖,則下列說法錯誤的是( )
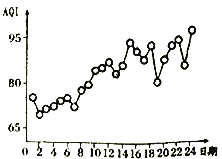
A. 該地區在該月2日空氣質量最好
B. 該地區在該月24日空氣質量最差
C. 該地區從該月7日到12日![]() 持續增大
持續增大
D. 該地區的空氣質量指數![]() 與這段日期成負相關
與這段日期成負相關
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com