
【題目】《復(fù)仇者聯(lián)盟4:終局之戰(zhàn)》是安東尼·羅素和喬·羅素執(zhí)導(dǎo)的美國科幻電影,改編自美國漫威漫畫,自2019年4月24日上映以來票房火爆.某電影院為了解在該影院觀看《復(fù)仇者聯(lián)盟4》的觀眾的年齡構(gòu)成情況,隨機(jī)抽取了100名觀眾的年齡,并分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 七組,得到如圖所示的頻率分布直方圖.
七組,得到如圖所示的頻率分布直方圖.
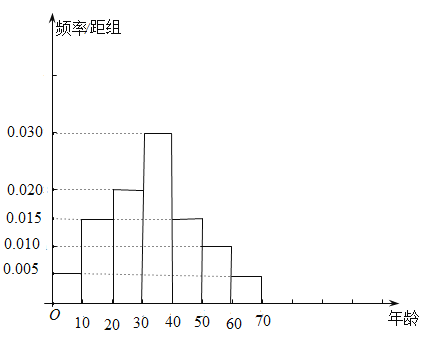
(1)求這100名觀眾年齡的平均數(shù)(同一組數(shù)據(jù)用該區(qū)間的中點(diǎn)值作代表)、中位數(shù);
(2)該電影院擬采用抽獎(jiǎng)活動(dòng)來增加趣味性,觀眾可以選擇是否參與抽獎(jiǎng)活動(dòng)(不參與抽獎(jiǎng)活動(dòng)按原價(jià)購票),活動(dòng)方案如下:每張電影票價(jià)格提高10元,同時(shí)購買這樣電影票的每位觀眾可獲得3次抽獎(jiǎng)機(jī)會(huì),中獎(jiǎng)1次則獎(jiǎng)勵(lì)現(xiàn)金![]() 元,中獎(jiǎng)2次則獎(jiǎng)勵(lì)現(xiàn)金
元,中獎(jiǎng)2次則獎(jiǎng)勵(lì)現(xiàn)金![]() 元,中獎(jiǎng)三次則獎(jiǎng)勵(lì)現(xiàn)金
元,中獎(jiǎng)三次則獎(jiǎng)勵(lì)現(xiàn)金![]() 元,其中
元,其中![]() 且
且![]() ,已知觀眾每次中獎(jiǎng)的概率均為
,已知觀眾每次中獎(jiǎng)的概率均為![]() .
.
①以某觀眾三次抽獎(jiǎng)所獲得的獎(jiǎng)金總額的數(shù)學(xué)期望為評(píng)判依據(jù),若要使抽獎(jiǎng)方案對(duì)電影院有利,則![]() 最高可定為多少;
最高可定為多少;
②據(jù)某時(shí)段內(nèi)的統(tǒng)計(jì),當(dāng)![]() 時(shí)該電影院有600名觀眾選擇參加抽獎(jiǎng)活動(dòng),并且
時(shí)該電影院有600名觀眾選擇參加抽獎(jiǎng)活動(dòng),并且![]() 每增加1元,則參加抽獎(jiǎng)活動(dòng)的觀眾增加100人.設(shè)該時(shí)間段內(nèi)觀影的總?cè)藬?shù)不變,抽獎(jiǎng)活動(dòng)給電影院帶來的利潤(rùn)的期望為
每增加1元,則參加抽獎(jiǎng)活動(dòng)的觀眾增加100人.設(shè)該時(shí)間段內(nèi)觀影的總?cè)藬?shù)不變,抽獎(jiǎng)活動(dòng)給電影院帶來的利潤(rùn)的期望為![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)①
;(2)①![]() 最高定為17元,才能使抽獎(jiǎng)方案對(duì)電影院有利,②
最高定為17元,才能使抽獎(jiǎng)方案對(duì)電影院有利,②![]() 時(shí)利潤(rùn)
時(shí)利潤(rùn)![]() 最大,為
最大,為![]() .
.
【解析】
(1)由頻率分布直方圖求平均數(shù)以及中位數(shù)的方法求解即可;
(2)①設(shè)觀眾三次抽獎(jiǎng)所獲得的獎(jiǎng)金總額為隨機(jī)變量![]() ,
,![]() 可能的取值為0,
可能的取值為0,![]() ,
,![]() ,
,![]() ,求出
,求出![]() 可能取值對(duì)應(yīng)的概率,得出期望,使期望小于等于10,得出對(duì)電影院有利時(shí)
可能取值對(duì)應(yīng)的概率,得出期望,使期望小于等于10,得出對(duì)電影院有利時(shí)![]() 的最大值;
的最大值;
②由期望的值以及題設(shè)條件得出![]() 的表達(dá)式,根據(jù)二次函數(shù)的性質(zhì),得出
的表達(dá)式,根據(jù)二次函數(shù)的性質(zhì),得出![]() 的最大值.
的最大值.
(1)平均數(shù)![]()
![]()
![]()
![]() ,
,
前三組的頻率之和為![]()
前四組為![]()
故中位數(shù)落在第4組
設(shè)中位數(shù)為![]() ,則
,則![]()
解得![]() ,即中位數(shù)為
,即中位數(shù)為![]() .
.
(2)①設(shè)觀眾三次抽獎(jiǎng)所獲得的獎(jiǎng)金總額為隨機(jī)變量![]() ,
,![]() 可能的取值為0,
可能的取值為0,![]() ,
,![]() ,
,![]()

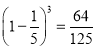
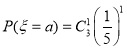
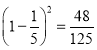
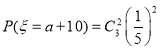
![]()
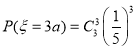
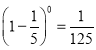
所以,![]()
![]()
令![]() ,解得
,解得![]()
所以![]() 最高定為17元,才能使抽獎(jiǎng)方案對(duì)電影院有利.
最高定為17元,才能使抽獎(jiǎng)方案對(duì)電影院有利.
②![]()
![]()
![]()
![]() .
.
![]() 為二次函數(shù),其對(duì)稱軸
為二次函數(shù),其對(duì)稱軸![]()
![]() 時(shí),
時(shí),![]() ,
,![]() 時(shí),
時(shí),![]() .
.
![]() ,因此
,因此![]() 時(shí)利潤(rùn)
時(shí)利潤(rùn)![]() 最大,為
最大,為![]()


 口算能手系列答案
口算能手系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】乒乓球賽規(guī)定:一局比賽,雙方比分在10平前,一方連續(xù)發(fā)球2次后,對(duì)方再連續(xù)發(fā)球2次,依次輪換,每次發(fā)球,勝方得1分,負(fù)方得0分。設(shè)在甲、乙的比賽中,每次發(fā)球,甲發(fā)球得1分的概率為![]() ,乙發(fā)球得1分的概率為
,乙發(fā)球得1分的概率為![]() ,各次發(fā)球的勝負(fù)結(jié)果相互獨(dú)立,甲、乙的一局比賽中,甲先發(fā)球.則開始第4次發(fā)球時(shí),甲、乙的比分為1比2的概率為________.
,各次發(fā)球的勝負(fù)結(jié)果相互獨(dú)立,甲、乙的一局比賽中,甲先發(fā)球.則開始第4次發(fā)球時(shí),甲、乙的比分為1比2的概率為________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下表是一個(gè)“數(shù)陣”:
1 | ( ) | ( ) | ( ) | … |
| … |
( ) | 1 | ( ) | ( ) | … |
| … |
( ) | ( ) | ( ) | 1 | … |
| … |
… | … | … | … | … | … | … |
|
|
|
| … |
| … |
… | … | … | … | … | … | … |
其中每行都是公差不為0等差數(shù)列,每列都是等比數(shù)列,![]() 表示位于第i行第j列的數(shù).
表示位于第i行第j列的數(shù).
(1)寫出![]() 的值:
的值:
(2)寫出![]() 的計(jì)算公式,以及第2020個(gè)1所在“數(shù)陣”中所在的位置.
的計(jì)算公式,以及第2020個(gè)1所在“數(shù)陣”中所在的位置.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】我國是世界上嚴(yán)重缺水的國家,某市政府為了鼓勵(lì)居民節(jié)約用水,計(jì)劃調(diào)整居民生活用水收費(fèi)方案,擬確定一個(gè)合理的月用水量標(biāo)準(zhǔn)![]() (噸)、一位居民的月用水量不超過
(噸)、一位居民的月用水量不超過![]() 的部分按平價(jià)收費(fèi),超出
的部分按平價(jià)收費(fèi),超出![]() 的部分按議價(jià)收費(fèi).為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數(shù)據(jù)按照[0,0.5),[0.5,1),…,[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.
的部分按議價(jià)收費(fèi).為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數(shù)據(jù)按照[0,0.5),[0.5,1),…,[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.

(Ⅰ)求直方圖中a的值;
(Ⅱ)設(shè)該市有30萬居民,估計(jì)全市居民中月均用水量不低于3噸的人數(shù),并說明理由;
(Ⅲ)若該市政府希望使85%的居民每月的用水量不超過標(biāo)準(zhǔn)![]() (噸),估計(jì)
(噸),估計(jì)![]() 的值,并說明理由.
的值,并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】有以下說法:
①一年按365天計(jì)算,兩名學(xué)生的生日相同的概率是![]() ;②買彩票中獎(jiǎng)的概率為0.001,那么買1 000張彩票就一定能中獎(jiǎng);③乒乓球賽前,決定誰先發(fā)球,抽簽方法是從1~10共10個(gè)數(shù)字中各抽取1個(gè),再比較大小,這種抽簽方法是公平的;④昨天沒有下雨,則說明“昨天氣象局的天氣預(yù)報(bào)降水概率是90%”是錯(cuò)誤的.
;②買彩票中獎(jiǎng)的概率為0.001,那么買1 000張彩票就一定能中獎(jiǎng);③乒乓球賽前,決定誰先發(fā)球,抽簽方法是從1~10共10個(gè)數(shù)字中各抽取1個(gè),再比較大小,這種抽簽方法是公平的;④昨天沒有下雨,則說明“昨天氣象局的天氣預(yù)報(bào)降水概率是90%”是錯(cuò)誤的.
根據(jù)我們所學(xué)的概率知識(shí),其中說法正確的序號(hào)是___.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (m
(m![]() R)
R)
(1)當(dāng)![]() 時(shí),
時(shí),
①求函數(shù)![]() 在x=1處的切線方程;
在x=1處的切線方程;
②求函數(shù)![]() 在
在![]() 上的最大,最小值.
上的最大,最小值.
(2)若函數(shù)![]() 在
在![]() 上單調(diào)遞增,求實(shí)數(shù)
上單調(diào)遞增,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}滿足:an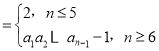 (n∈N*).若正整數(shù)k(k≥5)使得a12+a22+…+ak2=a1a2…ak成立,則k=( )
(n∈N*).若正整數(shù)k(k≥5)使得a12+a22+…+ak2=a1a2…ak成立,則k=( )
A.16B.17C.18D.19
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對(duì)于數(shù)列![]() ,若
,若![]() ,則稱數(shù)列
,則稱數(shù)列![]() 為“廣義遞增數(shù)列”,若
為“廣義遞增數(shù)列”,若![]() ,則稱數(shù)列
,則稱數(shù)列![]() 為“廣義遞減數(shù)列”,否則稱數(shù)列
為“廣義遞減數(shù)列”,否則稱數(shù)列![]() 為“擺動(dòng)數(shù)列”.已知數(shù)列
為“擺動(dòng)數(shù)列”.已知數(shù)列![]() 共4項(xiàng),且
共4項(xiàng),且![]() ,則數(shù)列
,則數(shù)列![]() 是擺動(dòng)數(shù)列的概率為______.
是擺動(dòng)數(shù)列的概率為______.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com