
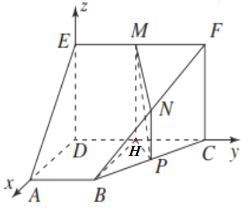
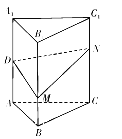
【題目】如圖所示的多面體的底面![]() 為直角梯形,四邊形
為直角梯形,四邊形![]() 為矩形,且
為矩形,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() ,
,![]() 的中點.
的中點.
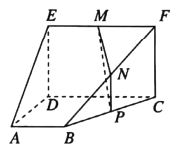
(1)求證:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)答案見解析.(2)![]()
【解析】
(1)先證明![]() 平面
平面![]() ,可得
,可得![]() ,取
,取![]() 中點
中點![]() ,利用等腰三角形的性質可得
,利用等腰三角形的性質可得![]() ,由線面垂直的判定即可得證;
,由線面垂直的判定即可得證;
(2)建立空間直角坐標系,求出各點坐標后,再求出平面![]() 的一個法向量
的一個法向量![]() 和直線
和直線![]() 的方向向量
的方向向量![]() ,求出兩向量夾角的余弦值后利用平方關系即可得解.
,求出兩向量夾角的余弦值后利用平方關系即可得解.
(1)證明:![]()
![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,
的中點,![]()
![]() ,
,
![]() 四邊形
四邊形![]() 為矩形,
為矩形,![]()
![]() ,
,
又![]()
![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,![]()
![]() ,
,
取![]() 中點
中點![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,
![]() 點
點![]() ,
,![]() ,
,![]() ,
,![]() 同在平面
同在平面![]() 內.
內.
在![]() 中,
中,![]() ,
,![]() ,
,![]() 為
為![]() 中點,
中點,
![]()
![]() ,
,
又![]()
![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() .
.
(2)由(1)知![]() ,
,![]() ,
,![]() 三條直線兩兩垂直且交于點
三條直線兩兩垂直且交于點![]() ,以
,以![]() 為原點,
為原點,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() ,
,![]() 軸,建立空間直角坐標系,如圖.
軸,建立空間直角坐標系,如圖.
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() 分別為
分別為![]() ,
,![]() 中點,可得
中點,可得![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的一個法向量為
的一個法向量為![]() ,則
,則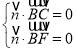 ,即
,即![]() ,
,
令![]() ,可得
,可得![]() ,
,![]() ,
,![]()
![]() ,
,
所以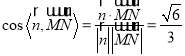 .
.
所以![]() 與平面
與平面![]() 所成角的余弦值為
所成角的余弦值為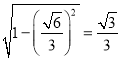 .
.


 優百分課時互動系列答案
優百分課時互動系列答案 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案科目:高中數學 來源: 題型:
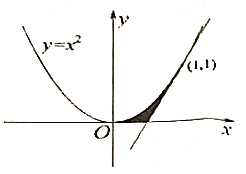
【題目】我國南北朝時期的數學家祖暅提出了計算體積的祖暅原理:“冪勢既同,則積不容異。”意思是:兩個等高的幾何體若在所有等高處的水平截面的面積相等,則這兩個幾何體的體積相等.已知曲線![]() ,直線
,直線![]() 為曲線
為曲線![]() 在點
在點![]() 處的切線.如圖所示,陰影部分為曲線
處的切線.如圖所示,陰影部分為曲線![]() 、直線
、直線![]() 以及
以及![]() 軸所圍成的平面圖形,記該平面圖形繞
軸所圍成的平面圖形,記該平面圖形繞![]() 軸旋轉一周所得的幾何體為
軸旋轉一周所得的幾何體為![]() .給出以下四個幾何體:
.給出以下四個幾何體:
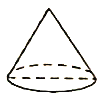
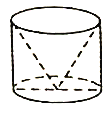


① ② ③ ④
圖①是底面直徑和高均為![]() 的圓錐;
的圓錐;
圖②是將底面直徑和高均為![]() 的圓柱挖掉一個與圓柱同底等高的倒置圓錐得到的幾何體;
的圓柱挖掉一個與圓柱同底等高的倒置圓錐得到的幾何體;
圖③是底面邊長和高均為![]() 的正四棱錐;
的正四棱錐;
圖④是將上底面直徑為![]() ,下底面直徑為
,下底面直徑為![]() ,高為
,高為![]() 的圓臺挖掉一個底面直徑為
的圓臺挖掉一個底面直徑為![]() ,高為
,高為![]() 的倒置圓錐得到的幾何體.
的倒置圓錐得到的幾何體.
根據祖暅原理,以上四個幾何體中與![]() 的體積相等的是( )
的體積相等的是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正三棱柱![]() 的各條棱長均相等,
的各條棱長均相等, ![]() 為
為![]() 的中點,
的中點, ![]() 分別是線段
分別是線段![]() 和線段
和線段![]() 上的動點(含端點),且滿足
上的動點(含端點),且滿足![]() .當
.當![]() 運動時,下列結論中不正確的是( )
運動時,下列結論中不正確的是( )
A. 平面![]() 平面
平面![]() B. 三棱錐
B. 三棱錐![]() 的體積為定值
的體積為定值
C. ![]() 可能為直角三角形 D. 平面
可能為直角三角形 D. 平面![]() 與平面
與平面![]() 所成的銳二面角范圍為
所成的銳二面角范圍為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() ,直線
,直線![]() 經過點
經過點![]() ,直線
,直線![]() 經過點
經過點![]() ,直線
,直線![]() 直線
直線![]() ,且直線
,且直線![]() 分別與橢圓
分別與橢圓![]() 相交于
相交于![]() 兩點和
兩點和![]() 兩點.
兩點.
(Ⅰ)若![]() 分別為橢圓
分別為橢圓![]() 的左、右焦點,且直線
的左、右焦點,且直線![]() 軸,求四邊形
軸,求四邊形![]() 的面積;
的面積;
(Ⅱ)若直線![]() 的斜率存在且不為0,四邊形
的斜率存在且不為0,四邊形![]() 為平行四邊形,求證:
為平行四邊形,求證:![]() ;
;
(Ⅲ)在(Ⅱ)的條件下,判斷四邊形![]() 能否為矩形,說明理由.
能否為矩形,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知:①函數![]() ;
;
②向量![]() ,
,![]() ,且
,且![]() ,
,![]() ;
;
③函數![]() 的圖象經過點
的圖象經過點![]()
請在上述三個條件中任選一個,補充在下面問題中,并解答.
已知_________________,且函數![]() 的圖象相鄰兩條對稱軸之間的距離為
的圖象相鄰兩條對稱軸之間的距離為![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(2)求函數![]() 在
在![]() 上的單調遞減區間.
上的單調遞減區間.
注:如果選擇多個條件分別解答,按第一個解答計分.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=|2x+4|+|x-3|.
(1)解關于x的不等式f(x)<8;
(2)對于正實數a,b,函數g(x)=f(x)-3a-4b只有一個零點,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com