
【題目】定義:若函數![]() 在區間
在區間![]() 上的值域為
上的值域為![]() ,則稱區間
,則稱區間![]() 是函數
是函數![]() 的“完美區間”,另外,定義區間
的“完美區間”,另外,定義區間![]() 的“復區間長度”為
的“復區間長度”為![]() ,已知函數
,已知函數![]() ,則( )
,則( )
A.![]() 是
是![]() 的一個“完美區間”
的一個“完美區間”
B. 是
是![]() 的一個“完美區間”
的一個“完美區間”
C.![]() 的所有“完美區間”的“復區間長度”的和為
的所有“完美區間”的“復區間長度”的和為![]()
D.![]() 的所有“完美區間”的“復區間長度”的和為
的所有“完美區間”的“復區間長度”的和為![]()
【答案】AC
【解析】
根據定義,當![]() 時求得
時求得![]() 的值域,即可判斷A;對于B,結合函數值域特點即可判斷;對于C、D,討論
的值域,即可判斷A;對于B,結合函數值域特點即可判斷;對于C、D,討論![]() 與
與![]() 兩種情況,分別結合定義求得“復區間長度”,即可判斷選項.
兩種情況,分別結合定義求得“復區間長度”,即可判斷選項.
對于A,當![]() 時,
時,![]() ,則其值域為
,則其值域為![]() ,滿足定義域與值域的范圍相同,因而滿足“完美區間”定義,所以A正確;
,滿足定義域與值域的范圍相同,因而滿足“完美區間”定義,所以A正確;
對于B,因為函數![]() ,所以其值域為
,所以其值域為![]() ,而
,而![]() ,所以不存在定義域與值域范圍相同情況,所以B錯誤;
,所以不存在定義域與值域范圍相同情況,所以B錯誤;
對于C,由定義域為![]() ,可知
,可知![]() ,
,
當![]() 時,
時,![]() ,此時
,此時![]() ,所以
,所以![]() 在
在![]() 內單調遞減,
內單調遞減,
則滿足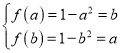 ,化簡可得
,化簡可得![]() ,
,
即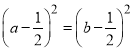 ,所以
,所以![]() 或
或![]() ,
,
解得![]() (舍)或
(舍)或![]() ,
,
由![]() 解得
解得![]() 或
或![]() (舍),
(舍),
所以![]() ,經檢驗滿足原方程組,所以此時完美區間為
,經檢驗滿足原方程組,所以此時完美區間為![]() ,則“復區間長度”為
,則“復區間長度”為![]() ;
;
當![]() 時,①若
時,①若![]() ,則
,則![]() ,此時
,此時![]() .當
.當![]() 在
在![]() 的值域為
的值域為![]() ,則
,則![]() ,因為
,因為![]() ,所以
,所以![]() ,即滿足
,即滿足![]() ,解得
,解得![]() ,
,![]() (舍).所以此時完美區間為
(舍).所以此時完美區間為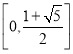 ,則“復區間長度”為
,則“復區間長度”為![]() ;
;
②若![]() ,則
,則![]() ,
,![]() ,此時
,此時![]() 在
在![]() 內單調遞增,若
內單調遞增,若![]() 的值域為
的值域為![]() ,則
,則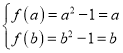 ,則
,則![]() 為方程
為方程![]() 的兩個不等式實數根,
的兩個不等式實數根,
解得![]() ,
,![]() , 所以
, 所以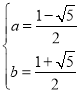 ,與
,與![]() 矛盾,所以此時不存在完美區間.
矛盾,所以此時不存在完美區間.
綜上可知,函數![]() 的“復區間長度”的和為
的“復區間長度”的和為![]() ,所以C正確,D錯誤;
,所以C正確,D錯誤;
故選:AC.


科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),在以坐標原點為極點,
為參數),在以坐標原點為極點,![]() 軸的正半軸為極軸的極坐標系中,直線
軸的正半軸為極軸的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若直線![]() 與曲線
與曲線![]() 至多只有一個公共點,求實數
至多只有一個公共點,求實數![]() 的取值范圍;
的取值范圍;
(2)若直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,且
兩點,且![]() ,
,![]() 的中點為
的中點為![]() ,求點
,求點![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() 為參數),在以坐標原點
為參數),在以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸的極坐標系中,點
軸的正半軸為極軸的極坐標系中,點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的直角坐標方程與曲線
的直角坐標方程與曲線![]() 的普通方程;
的普通方程;
(2)若![]() 是曲線
是曲線![]() 上的動點,
上的動點,![]() 為線段
為線段![]() 的中點,求點
的中點,求點![]() 到直線
到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E:![]() (
(![]() )的焦距為
)的焦距為![]() ,直線
,直線![]() :
:![]() 與x軸的交點為G,過點
與x軸的交點為G,過點![]() 且不與x軸重合的直線
且不與x軸重合的直線![]() 交E于點A,B.當
交E于點A,B.當![]() 垂直x軸時,
垂直x軸時,![]() 的面積為
的面積為![]() .
.
(1)求E的方程;
(2)若![]() ,垂足為C,直線
,垂足為C,直線![]() 交x軸于點D,證明:
交x軸于點D,證明:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
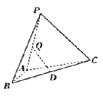
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,將
,將![]() 繞邊AB翻轉至
繞邊AB翻轉至![]() ,使面
,使面![]() 面ABC,D是BC的中點,設Q是線段PA上的動點,則當PC與DQ所成角取得最小值時,線段AQ的長度為( )
面ABC,D是BC的中點,設Q是線段PA上的動點,則當PC與DQ所成角取得最小值時,線段AQ的長度為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一對夫婦為了給他們的獨生孩子支付將來上大學的費用,從孩子一周歲生日開始,每年到銀行儲蓄![]() 元一年定期,若年利率為
元一年定期,若年利率為![]() 保持不變,且每年到期時存款(含利息)自動轉為新的一年定期,當孩子18歲生日時不再存入,將所有存款(含利息)全部取回,則取回的錢的總數為
保持不變,且每年到期時存款(含利息)自動轉為新的一年定期,當孩子18歲生日時不再存入,將所有存款(含利息)全部取回,則取回的錢的總數為![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com