
【題目】在四棱錐![]() 中,
中,![]() .
.
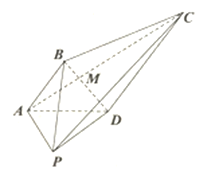
(1)設![]() 與
與![]() 相交于點
相交于點![]() ,
,![]() ,且
,且![]() 平面
平面![]() ,求實數
,求實數![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1) ![]() (2)
(2)![]()
【解析】
(1)由AB∥CD,得到![]() ,由MN∥平面PCD,得MN∥PC,從而
,由MN∥平面PCD,得MN∥PC,從而![]() ,由此能實數m的值.
,由此能實數m的值.
(2)由AB=AD,∠BAD=60°,知△ABD為等邊三角形,推導出PD⊥DB,PD⊥AD,從而PD⊥平面ABCD,以D為坐標原點,![]() 的方向為x,y軸的正方向建立空間直角坐標系,由此能求出二面角B﹣PC﹣D的余弦值.
的方向為x,y軸的正方向建立空間直角坐標系,由此能求出二面角B﹣PC﹣D的余弦值.
(1)因為![]() ,所以
,所以![]() .
.
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() .
.
所以![]() ,即
,即![]() .
.
(2)因為![]() ,可知三角形ABD為等邊三角形,
,可知三角形ABD為等邊三角形,
所以![]() ,又
,又![]() ,故
,故![]() ,所有
,所有![]() .
.
由已知![]() ,所以
,所以![]() 平面
平面![]() ,
,
如圖,以![]() 為坐標原點,
為坐標原點,![]() 的方向為
的方向為![]() 軸的正方向建立空間直角坐標系,
軸的正方向建立空間直角坐標系,

設![]() ,則
,則![]() ,
,
所以![]() ,
,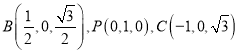
則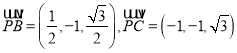 ,
,![]()
設平面![]() 的一個法向量為
的一個法向量為![]() ,則有
,則有
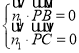 即
即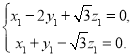 令
令![]() ,則
,則![]() ,即
,即![]() ,
,
設平面![]() 的一個法向量為
的一個法向量為![]() ,則有
,則有
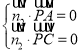 即
即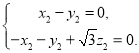 令
令![]() ,則
,則![]() ,即
,即![]() .
.
所以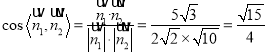 ,
,
設二面角![]() 的平面角為
的平面角為![]() ,則
,則![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,某山地車訓練中心有一直角梯形森林區域![]() ,其四條邊均為道路,其中
,其四條邊均為道路,其中![]() ,
,![]() ,
,![]() 千米,
千米,![]() 千米,
千米,![]() 千米.現有甲、乙兩名特訓隊員進行野外對抗訓練,要求同時從
千米.現有甲、乙兩名特訓隊員進行野外對抗訓練,要求同時從![]() 地出發勻速前往
地出發勻速前往![]() 地,其中甲的行駛路線是
地,其中甲的行駛路線是![]() ,速度為
,速度為![]() 千米/小時,乙的行駛路線是
千米/小時,乙的行駛路線是![]() ,速度為
,速度為![]() 千米/小時.
千米/小時.
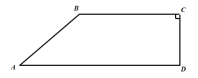
(1)若甲、乙兩名特訓隊員到達![]() 地的時間相差不超過
地的時間相差不超過![]() 分鐘,求乙的速度
分鐘,求乙的速度![]() 的取值范圍;
的取值范圍;
(2)已知甲、乙兩名特訓隊員攜帶的無線通訊設備有效聯系的最大距離是![]() 千米.若乙先于甲到達
千米.若乙先于甲到達![]() 地,且乙從
地,且乙從![]() 地到
地到![]() 地的整個過程中始終能用通訊設備對甲保持有效聯系,求乙的速度
地的整個過程中始終能用通訊設備對甲保持有效聯系,求乙的速度![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為確定下一年度投入某種產品的宣傳費,需了解年宣傳費![]() (單位:萬元)對年銷售量
(單位:萬元)對年銷售量![]() (單位:噸)和年利潤
(單位:噸)和年利潤![]() (單位:萬元)的影響.對近六年的年宣傳費
(單位:萬元)的影響.對近六年的年宣傳費![]() 和年銷售量
和年銷售量![]() (
(![]() )的數據作了初步統計,得到如下數據:
)的數據作了初步統計,得到如下數據:
年份 |
|
|
|
|
|
|
年宣傳費 |
|
|
|
|
|
|
年銷售量 |
|
|
|
|
|
|
經電腦模擬,發現年宣傳費![]() (萬元)與年銷售量
(萬元)與年銷售量![]() (噸)之間近似滿足關系式
(噸)之間近似滿足關系式![]() (
(![]() ).對上述數據作了初步處理,得到相關的值如表:
).對上述數據作了初步處理,得到相關的值如表:
|
|
|
|
|
|
|
|
(1)根據所給數據,求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(2)已知這種產品的年利潤![]() 與
與![]() ,
,![]() 的關系為
的關系為![]() 若想在
若想在![]() 年達到年利潤最大,請預測
年達到年利潤最大,請預測![]() 年的宣傳費用是多少萬元?
年的宣傳費用是多少萬元?
附:對于一組數據![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 中的斜率和截距的最小二乘估計分別為
中的斜率和截距的最小二乘估計分別為 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】己知數列![]() :1,
:1,![]() ,
,![]() ,3,3,3,
,3,3,3,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,即當
,即當![]() (
(![]() )時,
)時,![]() ,記
,記![]() (
(![]() ).
).
(1)求![]() 的值;
的值;
(2)求當![]() (
(![]() ),試用n、k的代數式表示
),試用n、k的代數式表示![]() (
(![]() );
);
(3)對于![]() ,定義集合
,定義集合![]() 是
是![]() 的整數倍,
的整數倍,![]() ,且
,且![]() ,求集合
,求集合![]() 中元素的個數.
中元素的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點到準線的距離為
的焦點到準線的距離為![]() ,直線
,直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,過這兩點分別作拋物線
兩點,過這兩點分別作拋物線![]() 的切線,且這兩條切線相交于點
的切線,且這兩條切線相交于點![]() .
.
(1)若![]() 的坐標為
的坐標為![]() ,求
,求![]() 的值;
的值;
(2)設線段![]() 的中點為
的中點為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,過
,過![]() 的直線
的直線![]() 與線段
與線段![]() 為直徑的圓相切,切點為
為直徑的圓相切,切點為![]() ,且直線
,且直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com