
【題目】已知橢圓![]() 的左右頂點分別為
的左右頂點分別為![]() ,左焦點為
,左焦點為![]() ,已知橢圓
,已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若過點![]() 的直線與該橢圓
的直線與該橢圓![]() 交于
交于![]() 兩點,且線段
兩點,且線段![]() 的中點恰為點
的中點恰為點![]() ,且直線
,且直線![]() 的方程;
的方程;
(3)若經過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,記
兩點,記![]() 與
與![]() 的面積分別為
的面積分別為![]() 和
和![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根據橢圓的離心率公式將P代入橢圓方程,即可求得a和b的值,求得橢圓方程;(2)利用點差法即可求出直線PQ的方程.(3)分類討論,設直線l的方程,代入橢圓方程,利用韋達定理及基本不等式的性質,即可求得|S1-S2|的取值范圍.
(1)因為e=![]() =
=![]() =
=![]() ,則3a2=4b2,將(1,
,則3a2=4b2,將(1,![]() )代入橢圓方程:
)代入橢圓方程:![]() +
+![]() =1,解得:a=2,b=
=1,解得:a=2,b=![]() ,所以橢圓方程為
,所以橢圓方程為![]() +
+![]() =1;
=1;
(2)設P(xP,yP),Q(xQ,yQ),∵線段PQ的中點恰為點N,∴xP+xQ=2,yP+yQ=2,
∵![]() +
+![]() =1,
=1,![]() +
+![]() =1,兩式相減可得
=1,兩式相減可得![]() (xP+xQ)(xP﹣xQ)+
(xP+xQ)(xP﹣xQ)+![]() (yP+yQ)(yP﹣yQ)=0,∴
(yP+yQ)(yP﹣yQ)=0,∴![]() =﹣
=﹣![]() ,即直線PQ的斜率為﹣
,即直線PQ的斜率為﹣![]() ,∴直線PQ的方程為y﹣1=﹣
,∴直線PQ的方程為y﹣1=﹣![]() (x﹣1),即3x+4y﹣7=0.
(x﹣1),即3x+4y﹣7=0.
(3)當直線l無斜率時,直線方程為x=1,此時C(1,﹣![]() ),D(1,
),D(1,![]() ),△ABD,△ABC面積相等,|S1﹣S2|=0,
),△ABD,△ABC面積相等,|S1﹣S2|=0,
當直線l斜率存在(顯然k≠0)時,設直線方程為y=k(x﹣1),
設C(x1,y1),D(x2,y2),聯立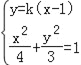 ,消掉y得(3+4k2)x2+8k2x+4k2﹣12=0,
,消掉y得(3+4k2)x2+8k2x+4k2﹣12=0,
顯然△>0,方程有根,且x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
此時|S1﹣S2|=2|y2|﹣|y1|=2|y2+y1|=![]() ,
,
因為k≠0,則|S1﹣S2|=![]() =
=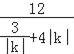 ≤
≤![]() =
=![]() ,(k=±
,(k=±![]() 時等號成立)
時等號成立)
所以|S1﹣S2|的最大值為![]() ,則0≤|S1﹣S2|≤
,則0≤|S1﹣S2|≤![]() ,
,
∴|S1﹣S2|的取值范圍[0,![]() ].
].


科目:高中數學 來源: 題型:
【題目】如圖,在五面體ABCDPN中,棱PA⊥面ABCD,AB=AP=2PN,底面ABCD是菱形,∠BAD=![]() .
.

(1)求證:PN∥AB;
(2)求NC與平面BDN所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設{an}是等比數列,則下列結論中正確的是( )
A. 若a1=1,a5=4,則a3=﹣2
B. 若a1+a3>0,則a2+a4>0
C. 若a2>a1,則a3>a2
D. 若a2>a1>0,則a1+a3>2a2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱臺ABC﹣A1B1C1中,D,E分別是AB,AC的中點,B1E⊥平面ABC,△AB1C是等邊三角形,AB=2A1B1,AC=2BC,∠ACB=90°.
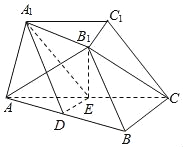
(1)證明:B1C∥平面A1DE;
(2)求二面角A﹣BB1﹣C的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右兩個焦點為
的左右兩個焦點為![]() ,離心率為
,離心率為![]() ,過點
,過點![]() .
.
(1)求橢圓C的標準方程;
(2)設直線![]() 與橢圓C相交于
與橢圓C相交于![]() 兩點,橢圓的左頂點為
兩點,橢圓的左頂點為![]() ,連接
,連接![]() 并延長交直線
并延長交直線![]() 于
于![]() 兩點 ,
兩點 ,![]() 分別為
分別為![]() 的縱坐標,且滿足
的縱坐標,且滿足![]() .求證:直線
.求證:直線![]() 過定點.
過定點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com