
【題目】如圖,菱形![]() 與等邊
與等邊![]() 所在平面互相垂直,
所在平面互相垂直,![]() ,
,![]() ,
,![]() ,
,![]() 分別是線段
分別是線段![]() ,
,![]() 的中點.
的中點.
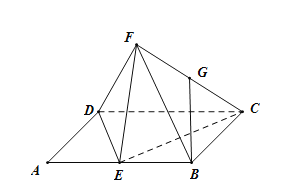
(1)求證:![]() 平面
平面![]() ;
;
(2)求點![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)證明見解析(2)![]() .
.
【解析】
(1)法一:通過構造平行四邊形的方法,證得![]() 平面
平面![]() ;法二:通過構造面面平行的方法,證得
;法二:通過構造面面平行的方法,證得![]() 平面
平面![]() .
.
(2)利用等體積法,計算出點![]() 到平面
到平面![]() 的距離.
的距離.
(1)法一:如圖,取線段![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() 是線段
是線段![]() 的中點,
的中點,
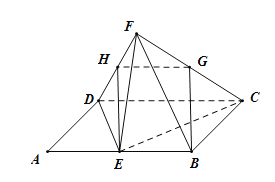
則![]() 且
且![]() .
.
在菱形![]() 中
中![]() 為線段
為線段![]() 中點,
中點,
則![]() 且
且![]() .
.
則![]() 且
且![]() ,
,
故四邊形![]() 為平行四邊形,
為平行四邊形,
所以![]() .
.
又因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
法二:如圖,取線段![]() 中點
中點![]() ,連接
,連接![]() ,
,![]() ,
,

在![]() 中,
中,![]() ,
,
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
在菱形![]() 中,
中,![]() ,
,
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又因為![]() ,且
,且![]() ,
,![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
因為![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)如圖,在等邊![]() 中取
中取![]() 邊中點
邊中點![]() ,連接
,連接![]() ,
,
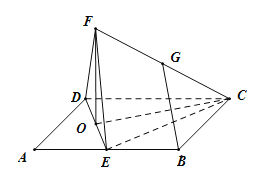
則![]() ,
,
因為平面![]() 平面
平面![]() 且平面
且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
在菱形![]() 中,
中,![]() ,
,![]() 是線段
是線段![]() 的中點,
的中點,
所以![]() .
.
連接![]() ,在
,在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() .
.
設點![]() 到平面
到平面![]() 的距離為
的距離為![]() ,
,
則![]() ,即
,即![]() ,
,
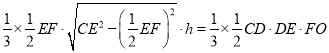 ,
,
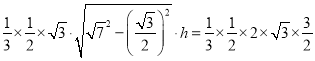 ,
,
解得![]() ,所以點
,所以點![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 1(a>b>0)的右焦點為F,離心率為
1(a>b>0)的右焦點為F,離心率為![]() ,且有3a2=4b2+1.
,且有3a2=4b2+1.
(1)求橢圓C的標準方程;
(2)過點F的直線l與橢圓C交于M,N兩點,過點M作直線x=3的垂線,垂足為點P,證明直線NP經過定點,并求出這個定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在創建“全國衛生文明城”的過程中,環保部門對某市市民進行了一次垃圾分類知識的網絡問卷調查,每一位市民僅有一次參加機會,通過隨機抽樣,得到參加問卷調查的1000人的得分(滿分:100分)數據,統計結果如下表所示.
組別 |
|
|
|
|
|
|
|
頻數 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(Ⅰ)已知此次問卷調查的得分![]() 服從正態分布
服從正態分布![]() ,
,![]() 近似為這1000人得分的平均值(同一組中的數據用該組區間的中點值為代表),請利用正態分布的知識求
近似為這1000人得分的平均值(同一組中的數據用該組區間的中點值為代表),請利用正態分布的知識求![]() ;
;
(Ⅱ)在(Ⅰ)的條件下,環保部門為此次參加問卷調查的市民制定如下獎勵方案:
(i)得分不低于![]() 的可以獲贈2次隨機話費,得分低于
的可以獲贈2次隨機話費,得分低于![]() 的可以獲贈1次隨機話費;
的可以獲贈1次隨機話費;
(ii)每次贈送的隨機話費和相應的概率如下表.現市民甲要參加此次問卷調查,記![]() 為該市民參加問卷調查獲贈的話費,求
為該市民參加問卷調查獲贈的話費,求![]() 的分布列及數學期望.
的分布列及數學期望.
贈送的隨機話費(單位:元) | 20 | 40 |
概率 |
|
|
附:若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖1,在![]() 中,
中,![]() ,
,![]() ,E為
,E為![]() 中點.以
中點.以![]() 為折痕將
為折痕將![]() 折起,使點C到達點D的位置,且
折起,使點C到達點D的位置,且![]() 為直二面角,F是線段
為直二面角,F是線段![]() 上靠近A的三等分點,連結
上靠近A的三等分點,連結![]() ,
,![]() ,
,![]() ,如圖2.
,如圖2.
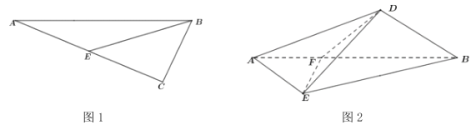
(1)證明:![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com