
【題目】已知![]() ,
,![]() .
.
(1)討論![]() 的單調區間;
的單調區間;
(2)當![]() 時,證明:
時,證明:![]() .
.
【答案】(1)![]() 在
在![]() 上單調遞減;在
上單調遞減;在![]() 和
和![]() 上單調遞增.(2)見解析
上單調遞增.(2)見解析
【解析】
(1)先求函數的定義域,再進行求導得![]() ,對
,對![]() 分成
分成![]() ,
,![]() ,
,![]() 三種情況討論,求得單調區間;
三種情況討論,求得單調區間;
(2)要證由![]() ,等價于證明
,等價于證明![]() ,再對
,再對![]() 分
分![]() ,
,![]() 兩種情況討論;證明當
兩種情況討論;證明當![]() 時,不等式成立,可先利用放縮法將參數
時,不等式成立,可先利用放縮法將參數![]() 消去,轉化成證明不等式
消去,轉化成證明不等式![]() 成立,再利用構造函數
成立,再利用構造函數![]() ,利用導數證明其最小值大于0即可。
,利用導數證明其最小值大于0即可。
(1)![]() 的定義域為
的定義域為![]() ,
,
![]() ,
,
當![]() 時,由
時,由![]() ,得
,得![]() ;
;
由![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增;
上單調遞增;
當![]() 時,由
時,由![]() ,得
,得![]() 或
或![]() ;
;
由![]() ,得
,得![]() ;
;
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 和
和![]() 上單調遞增;
上單調遞增;
當![]() 時,由
時,由![]() ,得
,得![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,由
時,由![]() ,得
,得![]() 或
或![]() ;由
;由![]() ,得
,得![]() ;
;
所以![]() 在
在![]() 上單調遞減;在
上單調遞減;在![]() 和
和![]() 上單調遞增.
上單調遞增.
(2)由![]() ,得
,得![]() ,
,
①當![]() 時,
時,![]() ,
,![]() ,不等式顯然成立;
,不等式顯然成立;
②當![]() 時,
時,![]() ,由
,由![]() ,得
,得![]() ,
,
所以只需證:![]() ,
,
即證![]() ,令
,令![]() ,
,
則![]() ,
,![]() ,
,
令![]() ,
,
則![]() ,
,
令![]() ,
,
則![]() ,
,
所以![]() 在
在![]() 上為增函數,
上為增函數,
因為![]() ,
,![]() ,
,
所以存在![]() ,
,![]() ,
,
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
又因為![]() ,
,![]() ,
,
當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞減,
上單調遞減,
當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() ,
,
所以![]() ,
,
所以原命題得證


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知三棱錐![]() 的四個頂點都在球
的四個頂點都在球![]() 的表面上,
的表面上,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,則:(1)球
,則:(1)球![]() 的表面積為__________;(2)若
的表面積為__________;(2)若![]() 是
是![]() 的中點,過點
的中點,過點![]() 作球
作球![]() 的截面,則截面面積的最小值是__________.
的截面,則截面面積的最小值是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
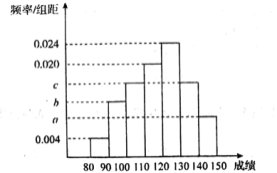
【題目】高三年級某班50名學生期中考試數學成績的頻率分布直方圖如圖所示,成績分組區間為:![]()
![]()
![]()
![]()
![]()
![]()
![]() .其中a,b,c成等差數列且
.其中a,b,c成等差數列且![]() .物理成績統計如表.(說明:數學滿分150分,物理滿分100分)
.物理成績統計如表.(說明:數學滿分150分,物理滿分100分)
分組 |
|
|
|
|
|
頻數 | 6 | 9 | 20 | 10 | 5 |
(1)根據頻率分布直方圖,請估計數學成績的平均分;
(2)根據物理成績統計表,請估計物理成績的中位數;
(3)若數學成績不低于140分的為“優”,物理成績不低于90分的為“優”,已知本班中至少有一個“優”同學總數為6人,從此6人中隨機抽取3人,記X為抽到兩個“優”的學生人數,求X的分布列和期望值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業擁有3條相同的生產線,每條生產線每月至多出現一次故障.各條生產線是否出現故障相互獨立,且出現故障的概率為![]() .
.
(1)求該企業每月有且只有1條生產線出現故障的概率;
(2)為提高生產效益,該企業決定招聘名維修工人及時對出現故障的生產線進行維修.已知每名維修工人每月只有及時維修1條生產線的能力,且每月固定工資為1萬元.此外,統計表明,每月在不出故障的情況下,每條生產線創造12萬元的利潤;如果出現故障能及時維修,每條生產線創造8萬元的利潤;如果出現故障不能及時維修,該生產線將不創造利潤,以該企業每月實際獲利的期望值為決策依據,在![]() 與
與![]() 之中選其一,應選用哪個?(實際獲利=生產線創造利潤-維修工人工資)
之中選其一,應選用哪個?(實際獲利=生產線創造利潤-維修工人工資)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖來自古希臘數學家希波克拉底所研究的幾何圖形.此圖由三個半圓構成,三個半圓的直徑分別為直角三角形ABC的斜邊BC,直角邊AB,AC.△ABC的三邊所圍成的區域記為I,黑色部分記為II,其余部分記為III.在整個圖形中隨機取一點,此點取自I,II,III的概率分別記為p1,p2,p3,則
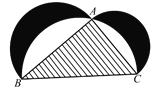
A. p1=p2 B. p1=p3
C. p2=p3 D. p1=p2+p3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() ,
,![]() 為其焦點,
為其焦點,![]() 為其準線,過
為其準線,過![]() 任作一條直線交拋物線于
任作一條直線交拋物線于![]() 兩點,
兩點,![]() 、
、![]() 分別為
分別為![]() 、
、![]() 在
在![]() 上的射影,
上的射影,![]() 為
為![]() 的中點,給出下列命題:
的中點,給出下列命題:
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
(4)![]() 與
與![]() 的交點的
的交點的![]() 軸上;(5)
軸上;(5)![]() 與
與![]() 交于原點.
交于原點.
其中真命題的序號為_________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱![]() 的側面
的側面![]() 是正方形,平面
是正方形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,點
,點![]() 在
在![]() 上,
上,![]() ,
,![]() 是
是![]() 的中點.
的中點.
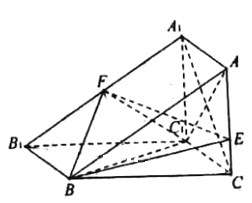
(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)判斷平面![]() 與平面
與平面![]() 是否垂直,直接寫出結論,不必說明理由;
是否垂直,直接寫出結論,不必說明理由;
(Ⅲ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數g(x)=![]() ,f(x)=g'(x)-
,f(x)=g'(x)-![]() (a是常數).若對a∈R,函數h(x)=kx(k是常數)的圖象與曲線y=f(x)總相切于一個定點.
(a是常數).若對a∈R,函數h(x)=kx(k是常數)的圖象與曲線y=f(x)總相切于一個定點.
(1)求k的值;
(2)若對![]() ∈(0,+∞),[f(
∈(0,+∞),[f(![]() )-h(
)-h(![]() )][f(
)][f(![]() )-h(
)-h(![]() )]>0,求實數a的取值范圍.
)]>0,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com